题目内容
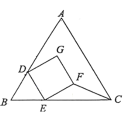
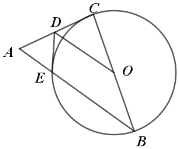
【题目】如图,已知在![]() 中,
中,![]() ,以BC为直径作
,以BC为直径作![]() 交
交![]() 于点
于点![]() ,
,![]() 为AC边的中点,连接
为AC边的中点,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)①若AC=3,AE=1,求![]() 的半径;
的半径;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
【答案】(1)详见解析;(2)①![]() ②
②![]()
【解析】
(1)连接OE、CE,由圆周角定理得出∠BEC=90°,则∠AEC=90°,由直角三角形斜边上的中线性质得出AD=CD=DE,由等腰三角形的性质得出∠DEC=∠DCE,∠OCE=∠OEC,证出∠OED=90°,即可得出结论;
(2)①由勾股定理求出CE=2![]() ,证△OCE∽△DAE,得出比例式,求出OC的长即可;
,证△OCE∽△DAE,得出比例式,求出OC的长即可;
②证△ABC是等腰直角三角形,得出∠ABC=45°,证四边形OCDE是矩形,由OC=OE,即可得出四边形OCDE是正方形.
(1)证明:连接OE、CE,如图所示:
∵BC是⊙O的直径,
∴∠BEC=90°,
∴∠AEC=90°,
∵D是AC的中点,
∴DE=![]() AC=AD=CD,
AC=AD=CD,
∴∠DEC=∠DCE,
∵OC=OE,
∴∠OCE=∠OEC,
∵∠ACB=90°,
∴∠DEC+∠OEC=∠DCE+∠OCE=∠ACB=90°,
∴∠OED=90°,即OE⊥DE,
∵E为⊙O上的点,
∴DE是⊙O的切线;
(2)解:①∵AC=3,
∴AD=DE=![]() AC=
AC=![]() ,
,
∵∠AEC=90°,
∴CE=![]() ,
,
∵∠BEC=90°,
∴∠CBE+∠OCE=90°,
∵∠ACB=90°,
∴∠CBE+∠DAE=90°,
∴∠OCE=∠DAE,
∵AD=DE,OC=OE,
∴∠OCE=∠OEC=∠DAE=∠DEA,
∴△OCE∽△DAE,
∴![]() ,
,
即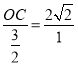 ,
,
解得:OC=![]() ,
,
故半径长为![]() ;
;
②当∠A=45°时,四边形OCDE是正方形;理由如下:
∵∠A=45°,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∵OB=OE,
∴∠OBE=∠OEB=45°,
∴∠COE=∠OBE+∠OEB=45°+45°=90°,
∵∠ACB=90°,∠OED=90°,
∴四边形OCDE是矩形,
∵OC=OE,
∴四边形OCDE是正方形;
故答案为:45°.