题目内容
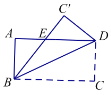
【题目】如图,矩形![]() 中,沿着直线
中,沿着直线![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于
于![]() ,
,![]() ,
,![]() ,则
,则![]() 的长是____.
的长是____.
【答案】10
【解析】
先根据翻折变换的性质得出CD=C′D,∠C=∠C′=90°,再设DE=x,则AE=16x,由全等三角形的判定定理得出Rt△ABE≌Rt△C′DE,可得出BE=DE=x,在Rt△ABE中利用勾股定理即可求出x的值,进而得出DE的长.
∵Rt△DC′B由Rt△DBC翻折而成,
∴CD=C′D=AB=8,∠C=∠C′=90°,
设DE=x,则AE=16x,
∵∠A=∠C′=90°,∠AEB=∠DEC′,
∴∠ABE=∠C′DE,
在Rt△ABE与Rt△C′DE中,
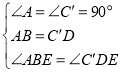 ,
,
∴Rt△ABE≌Rt△C′DE,
∴BE=DE=x,
在Rt△ABE中,
AB2+AE2=BE2,即82+(16x)2=x2,解得x=10,即DE=10.
故答案为:10.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目