Ő‚ńŅńŕ»›
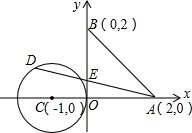
»ÁÕľ1°Ę2£¨“—÷™Ň◊őÔŌŖy=ax2+bx+3ĺ≠ĻżĶ„B£®-1£¨0£©°ĘC£®3£¨0£©£¨ĹĽy÷Š”ŕĶ„A£ģ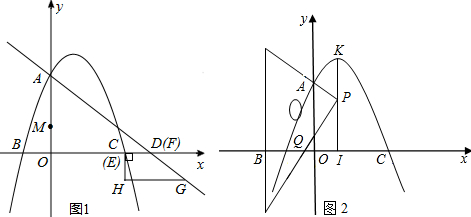
£®1£©«ůīňŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
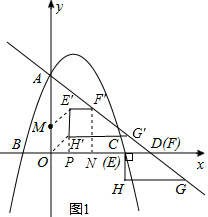
£®2£©»ÁÕľ1£¨»ŰM£®0£¨1£©£¨ĻżĶ„AĶń÷ĪŌŖ”Žx÷ŠĹĽ”ŕĶ„D£®4£¨0£©£ģ÷ĪĹ«Ő›–őEFGHĶń…ŌĶ◊EF”ŽŌŖ∂őCD÷ōļŌ£¨°ŌFEH=90°„£¨EF°őHG£¨EF=EH=1£ģ÷ĪĹ«Ő›–őEFGHī”Ķ„DŅ™ ľ£¨—ō…šŌŖDA∑ĹŌÚ‘»ňŔ‘ň∂Į£¨‘ň∂ĮĶńňŔ∂»ő™1łŲ≥§∂»Ķ•őĽ/√Ž£¨‘ŕ‘ň∂ĮĻż≥Ő÷–—ŁFG”Ž÷ĪŌŖAD ľ÷’÷ōļŌ£¨…Ť‘ň∂Į Īľšő™t√Ž£ģĶĪtő™ļő÷Ķ Ī£¨“‘M°ĘO°ĘH°ĘEő™∂•Ķ„ĶńňńĪŖ–ő «Őō ‚Ķń∆Ĺ––ňńĪŖ–ő£Ľ
£®3£©»ÁÕľ2£¨Ň◊őÔŌŖ∂•Ķ„ő™K£¨KI°Õx÷Š”ŕIĶ„£¨“ĽŅť»żĹ«įŚ÷ĪĹ«∂•Ķ„P‘ŕŌŖ∂őKI…ŌĽ¨∂Į£¨«““Ľ÷ĪĹ«ĪŖĻżAĶ„£¨ŃŪ“Ľ÷ĪĹ«ĪŖ”Žx÷ŠĹĽ”ŕQ£®m£¨0£©£¨«Ž«ů≥Ų Ķ żmĶńĪšĽĮ∑∂őߣ¨≤ĘňĶ√ųņŪ”…£ģ

£®1£©«ůīňŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©»ÁÕľ1£¨»ŰM£®0£¨1£©£¨ĻżĶ„AĶń÷ĪŌŖ”Žx÷ŠĹĽ”ŕĶ„D£®4£¨0£©£ģ÷ĪĹ«Ő›–őEFGHĶń…ŌĶ◊EF”ŽŌŖ∂őCD÷ōļŌ£¨°ŌFEH=90°„£¨EF°őHG£¨EF=EH=1£ģ÷ĪĹ«Ő›–őEFGHī”Ķ„DŅ™ ľ£¨—ō…šŌŖDA∑ĹŌÚ‘»ňŔ‘ň∂Į£¨‘ň∂ĮĶńňŔ∂»ő™1łŲ≥§∂»Ķ•őĽ/√Ž£¨‘ŕ‘ň∂ĮĻż≥Ő÷–—ŁFG”Ž÷ĪŌŖAD ľ÷’÷ōļŌ£¨…Ť‘ň∂Į Īľšő™t√Ž£ģĶĪtő™ļő÷Ķ Ī£¨“‘M°ĘO°ĘH°ĘEő™∂•Ķ„ĶńňńĪŖ–ő «Őō ‚Ķń∆Ĺ––ňńĪŖ–ő£Ľ
£®3£©»ÁÕľ2£¨Ň◊őÔŌŖ∂•Ķ„ő™K£¨KI°Õx÷Š”ŕIĶ„£¨“ĽŅť»żĹ«įŚ÷ĪĹ«∂•Ķ„P‘ŕŌŖ∂őKI…ŌĽ¨∂Į£¨«““Ľ÷ĪĹ«ĪŖĻżAĶ„£¨ŃŪ“Ľ÷ĪĹ«ĪŖ”Žx÷ŠĹĽ”ŕQ£®m£¨0£©£¨«Ž«ů≥Ų Ķ żmĶńĪšĽĮ∑∂őߣ¨≤ĘňĶ√ųņŪ”…£ģ
£®1£©°ŖŇ◊őÔŌŖy=ax2+bx+3ĺ≠ĻżĶ„B£®-1£¨0£©°ĘC£®3£¨0£©£¨
°ŗ
£¨
Ĺ‚Ķ√
£ģ
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y=-x2+2x+3£ģ
£®2£©ĶĪ÷ĪĹ«Ő›–őEFGH‘ň∂ĮĶĹE°šF°šG°šH°š Ī£¨ĻżĶ„F°š◊ųF°šN°Õx÷Š”ŕĶ„N£¨—”≥§E°šH°ĮĹĽx÷Š”ŕĶ„P£ģ
 °ŖĶ„MĶń◊ÝĪÍő™£®0£¨1£©£¨Ķ„A «Ň◊őÔŌŖ”Žy÷ŠĶńĹĽĶ„£¨
°ŖĶ„MĶń◊ÝĪÍő™£®0£¨1£©£¨Ķ„A «Ň◊őÔŌŖ”Žy÷ŠĶńĹĽĶ„£¨
°ŗĶ„AĶń◊ÝĪÍő™£®0£¨3£©£ģ
°ŖOA=3£¨OD=4£¨
°ŗAD=5£ģ
°ŖE°šH°š°őOM£¨E°šH°š=OM=1£¨
°ŗňńĪŖ–őE°šH°šOM «∆Ĺ––ňńĪŖ–ő£®ĶĪE°šH°š≤Ľ”Žy÷Š÷ōļŌ Ī£©£ģ
°ŖF°šN°őy÷Š£¨NG°š°őx÷Š£¨
°ŗ°ųF°šND°◊°ųAOD£ģ
°ŗ
=
=
£ģ
°Ŗ÷ĪĹ«Ő›–őE°šF°šG°šH°š «÷ĪĹ«Ő›–őEFGH—ō…šŌŖDA∑ĹŌÚ∆Ĺ“∆Ķ√ĶĹĶń£¨
°ŗF°šD=t£¨
°ŗ
=
=
£ģ
°ŗF°šN=
£¨ND=
£ģ
°ŖE°šF°š=PN=1£¨
°ŗOP=OD-PN-ND=4-1-
=3-
£ģ
°ŖE°šP=F°šN=
£¨E°šH°š=1£¨
°ŗH°šP=
-1£ģ
»Ű∆Ĺ––ňńĪŖ–őE°šH°šOM «ĺō–ő£¨‘Ú°ŌMOH°š=90°„£¨īň ĪH°šG°š”Žx÷Š÷ōļŌ£ģ
°ŖF°šD=t£¨
°ŗF°šN=
=1£¨ľīt=
£ģ
ľīĶĪt=
√Ž Ī£¨∆Ĺ––ňńĪŖ–őEHOM «ĺō–ő£ģ
»Ű∆Ĺ––ňńĪŖ–őE°šH°šOM «Ń‚–ő£¨‘ÚOH°š=1£ģ
‘ŕRt°ųH°šOP÷–£¨OP2+H°šP2=OH°š2£¨ľī(3-
)2+(
-1)2=12
Ķ√t2-6t+9=0£¨Ĺ‚Ķ√t1=t2=3£ģ
ľīĶĪt=3√Ž Ī£¨∆Ĺ––ňńĪŖ–őEHOM «Ń‚–ő£ģ
◊Ř…Ōňý Ų£¨ĶĪt=
√Ž Ī£¨∆Ĺ––ňńĪŖ–őEHOM «ĺō–ő£¨ĶĪt=3√Ž Ī£¨∆Ĺ––ňńĪŖ–őEHOM «Ń‚–ő£ģ
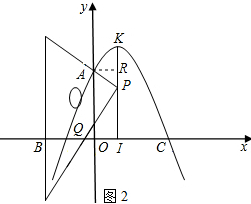 £®3£©ĻżA◊ųAR°ÕKI”ŕRĶ„£¨‘ÚAR=KR=1£ģ
£®3£©ĻżA◊ųAR°ÕKI”ŕRĶ„£¨‘ÚAR=KR=1£ģ
ĶĪQ‘ŕKI◊ů≤ŗ Ī£¨°ųARP°◊°ųPIQ£ģ
…ŤPI=n£¨‘ÚRP=3-n£¨
°ŗ
=
£¨ľīn2-3n-m+1=0£¨
°ŖĻō”ŕnĶń∑Ĺ≥Ő”–Ĺ‚£¨°ų=£®-3£©2-4£®-m+1£©°›0£¨
Ķ√m°›-
£Ľ
ĶĪQ‘ŕKI”“≤ŗ Ī£¨
Rt°ųAPQ÷–£¨AR=RK=1£¨°ŌAKI=45°„Ņ…Ķ√OQ=5£ģľīPő™Ķ„K Ī£¨
°ŗm°‹5£ģ
◊Ř…Ōňý Ų£¨mĶńĪšĽĮ∑∂őßő™£ļ-
°‹m°‹5£ģ
°ŗ
|
Ĺ‚Ķ√
|
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y=-x2+2x+3£ģ
£®2£©ĶĪ÷ĪĹ«Ő›–őEFGH‘ň∂ĮĶĹE°šF°šG°šH°š Ī£¨ĻżĶ„F°š◊ųF°šN°Õx÷Š”ŕĶ„N£¨—”≥§E°šH°ĮĹĽx÷Š”ŕĶ„P£ģ
 °ŖĶ„MĶń◊ÝĪÍő™£®0£¨1£©£¨Ķ„A «Ň◊őÔŌŖ”Žy÷ŠĶńĹĽĶ„£¨
°ŖĶ„MĶń◊ÝĪÍő™£®0£¨1£©£¨Ķ„A «Ň◊őÔŌŖ”Žy÷ŠĶńĹĽĶ„£¨°ŗĶ„AĶń◊ÝĪÍő™£®0£¨3£©£ģ
°ŖOA=3£¨OD=4£¨
°ŗAD=5£ģ
°ŖE°šH°š°őOM£¨E°šH°š=OM=1£¨
°ŗňńĪŖ–őE°šH°šOM «∆Ĺ––ňńĪŖ–ő£®ĶĪE°šH°š≤Ľ”Žy÷Š÷ōļŌ Ī£©£ģ
°ŖF°šN°őy÷Š£¨NG°š°őx÷Š£¨
°ŗ°ųF°šND°◊°ųAOD£ģ
°ŗ
| F°šN |
| AO |
| ND |
| OD |
| F°šD |
| AD |
°Ŗ÷ĪĹ«Ő›–őE°šF°šG°šH°š «÷ĪĹ«Ő›–őEFGH—ō…šŌŖDA∑ĹŌÚ∆Ĺ“∆Ķ√ĶĹĶń£¨
°ŗF°šD=t£¨
°ŗ
| F°šN |
| 3 |
| ND |
| 4 |
| t |
| 5 |
°ŗF°šN=
| 3t |
| 5 |
| 4t |
| 5 |
°ŖE°šF°š=PN=1£¨
°ŗOP=OD-PN-ND=4-1-
| 4t |
| 5 |
| 4t |
| 5 |
°ŖE°šP=F°šN=
| 3t |
| 5 |
°ŗH°šP=
| 3t |
| 5 |
»Ű∆Ĺ––ňńĪŖ–őE°šH°šOM «ĺō–ő£¨‘Ú°ŌMOH°š=90°„£¨īň ĪH°šG°š”Žx÷Š÷ōļŌ£ģ
°ŖF°šD=t£¨
°ŗF°šN=
| 3t |
| 5 |
| 5 |
| 3 |
ľīĶĪt=
| 5 |
| 3 |
»Ű∆Ĺ––ňńĪŖ–őE°šH°šOM «Ń‚–ő£¨‘ÚOH°š=1£ģ
‘ŕRt°ųH°šOP÷–£¨OP2+H°šP2=OH°š2£¨ľī(3-
| 4t |
| 5 |
| 3t |
| 5 |
Ķ√t2-6t+9=0£¨Ĺ‚Ķ√t1=t2=3£ģ
ľīĶĪt=3√Ž Ī£¨∆Ĺ––ňńĪŖ–őEHOM «Ń‚–ő£ģ
◊Ř…Ōňý Ų£¨ĶĪt=
| 5 |
| 3 |
 £®3£©ĻżA◊ųAR°ÕKI”ŕRĶ„£¨‘ÚAR=KR=1£ģ
£®3£©ĻżA◊ųAR°ÕKI”ŕRĶ„£¨‘ÚAR=KR=1£ģĶĪQ‘ŕKI◊ů≤ŗ Ī£¨°ųARP°◊°ųPIQ£ģ
…ŤPI=n£¨‘ÚRP=3-n£¨
°ŗ
| 1-m |
| 3-n |
| n |
| 1 |
°ŖĻō”ŕnĶń∑Ĺ≥Ő”–Ĺ‚£¨°ų=£®-3£©2-4£®-m+1£©°›0£¨
Ķ√m°›-
| 5 |
| 4 |
ĶĪQ‘ŕKI”“≤ŗ Ī£¨
Rt°ųAPQ÷–£¨AR=RK=1£¨°ŌAKI=45°„Ņ…Ķ√OQ=5£ģľīPő™Ķ„K Ī£¨
°ŗm°‹5£ģ
◊Ř…Ōňý Ų£¨mĶńĪšĽĮ∑∂őßő™£ļ-
| 5 |
| 4 |

Ń∑Ōį≤ŠŌĶŃ–īūįł
ŌŗĻōŐ‚ńŅ

 «Ň◊őÔŌŖ∂‘≥∆÷Š…ŌĶń∂ĮĶ„£ģ
«Ň◊őÔŌŖ∂‘≥∆÷Š…ŌĶń∂ĮĶ„£ģ
 őÔŌŖy=
őÔŌŖy=