题目内容
如图,直线y=-
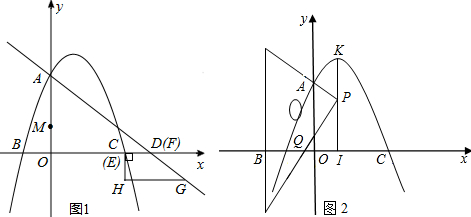
x经过抛物线y=ax2+8ax-3的顶点M,点P(x,y)是抛物线上的动点,点Q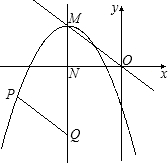 是抛物线对称轴上的动点.
是抛物线对称轴上的动点.
(1)求抛物线的解析式;
(2)当PQ∥OM时,设线段PQ的长为d,求d关于x的函数解析式;
(3)当以P、Q、O、M四点为顶点的四边形是平行四边形时,求P、Q两点的坐标.
| 3 |
| 4 |
 是抛物线对称轴上的动点.
是抛物线对称轴上的动点.(1)求抛物线的解析式;
(2)当PQ∥OM时,设线段PQ的长为d,求d关于x的函数解析式;
(3)当以P、Q、O、M四点为顶点的四边形是平行四边形时,求P、Q两点的坐标.
(1)抛物线y=ax2+8ax-3的顶点是(-4,-16a-3),代入y=-
x,
得到-16a-3=3,
解得a=-
因而函数是y=-
x2-3x-3
(2)∵a=-
,∴-16a-3=3,
∴抛物线y=-
x2-3x-3的顶点坐标是(-4,3),
设直线OM的解析式是y=kx,把x=-4,y=3代入得3=-4k,
解得k=-
,
点P(x,y)即(x,-
x2-3x-3),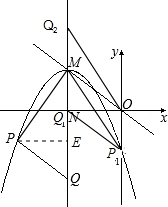
作PE⊥MQ于点E.则PE=x+4或-4-x.
∵PQ∥OM,
∴
=
∴
=
,
∴d=-
x-5或d=
x+5;
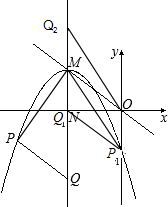
(3)如图P1,Q1时MP1=OQ1=3,直接得出点的坐标:
P1(0,-3),Q1(-4,0);
当MP2=OQ2=3时,直接得出点的坐标:P2(0,-3),Q2(-4,6);
∵MO=5,
∵根据点到直线的距离公式得到d=
x±5,
∴x=-8时,d=5,
∴P点的横坐标为-8,代入二次函数解析式求出纵坐标即可,
∴P(-8,-3),Q(-4,-6);
故答案为:P1(0,-3),Q1(-4,0);P2(0,-3),Q2(-4,6);P(-8,-3),Q(-4,-6).
| 3 |
| 4 |
得到-16a-3=3,
解得a=-
| 3 |
| 8 |
因而函数是y=-
| 3 |
| 8 |
(2)∵a=-
| 3 |
| 8 |
∴抛物线y=-
| 3 |
| 8 |
设直线OM的解析式是y=kx,把x=-4,y=3代入得3=-4k,
解得k=-
| 3 |
| 4 |
点P(x,y)即(x,-
| 3 |
| 8 |

作PE⊥MQ于点E.则PE=x+4或-4-x.
∵PQ∥OM,
∴
| EQ |
| PE |
| 3 |
| 4 |
∴
| PE |
| PQ |
| 4 |
| 5 |
∴d=-
| 5 |
| 4 |
| 5 |
| 4 |
(3)如图P1,Q1时MP1=OQ1=3,直接得出点的坐标:
P1(0,-3),Q1(-4,0);
当MP2=OQ2=3时,直接得出点的坐标:P2(0,-3),Q2(-4,6);
∵MO=5,
∵根据点到直线的距离公式得到d=
| 5 |
| 4 |
∴x=-8时,d=5,
∴P点的横坐标为-8,代入二次函数解析式求出纵坐标即可,
∴P(-8,-3),Q(-4,-6);
故答案为:P1(0,-3),Q1(-4,0);P2(0,-3),Q2(-4,6);P(-8,-3),Q(-4,-6).


练习册系列答案
相关题目

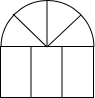
 及其内部的抛物线部分经过平移和对称变换得到的.
及其内部的抛物线部分经过平移和对称变换得到的.