Question

【题目】如图所示，一次函数(为常数)的图象与反比例函数(为常数，且<0)的图象交于A，B两点．

(1) 如图①，当，时，

① A ( ， )，B ( ， )；

②直接写出使成立的的取值范围；

(2) 如图②，将(1)中直线AB向下平移，交反比例函数图像于点C，D，连接OC，AC，若△AOC的面积为8，求的值；

(3) 若A，B两点的横坐标分别为，，且，满足，证明：2m-b=-3．

Answer 1

【答案】(1)①A(-2，2)，B(2，-2)；②或 ； (2)-8 ； (3)详见解析．

【解析】

（1）①当，时，代入解析式，联合方程组，即可求出A、B的坐标；

②利用图像法解不等式，即可得到答案；

（2）作OE⊥CD，先求出OA的长度，然后利用平行线之间的距离和三角形的面积，即可求出b的值；

（3）过点A作y轴的平行线，过点B作x轴的平行线，两平行线交于点F，设点A为（m，），点B为（n，），得到，求出点A、B，代入直线的方程，得到，结合，即可得到结论成立．

解：（1）①当，时，有

，，

令，则，

解得：，，

∴点A为（，2），点B为（2，）；

②∵，则由图可知，

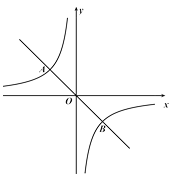
的取值范围是：或；

（2）作OE⊥CD，如图：

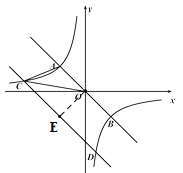
由图可知，（），，

∴OD=，

∵∠EDO=45°，

∴△ODE为等腰直角三角形，

∴，

∵，

解得：；

（3）证明：过点A作y轴的平行线，过点B作x轴的平行线，两平行线交于点F，如图，

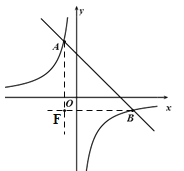
∵点A、B在反比例函数的图像上，

设点A为（m，），点B为（n，），

∵直线AB为，

∴∠ABF=45°，

∴△ABF为等腰直角三角形，

∴AF=BF=，

∴，

∴，

∴点A为（m，n），点B为（n，m），

∴，

∵，

∴，

∴．