题目内容
【题目】如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数![]() 的图象上.
的图象上.

(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
【答案】(1)m=3,k=12;(2)![]() 或
或![]()
【解析】
试题分析:(1)根据反比例函数图象上的点的坐标的特征可得![]() ,即可求得结果;
,即可求得结果;
(2)存在两种情况,①当M点在x轴的正半轴上,N点在y轴的正半轴上时,②当M点在x轴的负半轴上,N点在y轴的负半轴上时,根据平行四边形的性质求解即可.
(1)由题意可知,![]()
解得m1=3,m2=-1(舍去)
∴A(3,4),B(4,3);
∴k=4×3=12;
(2)存在两种情况,如图:
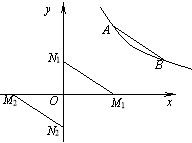
①当M点在x轴的正半轴上,N点在y轴的正半轴上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵四边形AN1M1B为平行四边形,
∴线段N1M1可看作由线段AB向左平移3个单位,再向下平移3个单位得到的
由(1)知A点坐标为(3,4),B点坐标为(4,3),
∴N1点坐标为(0,1),M1点坐标为(1,0)
设直线M1N1的函数表达式为![]() ,把x=1,y=0代入,解得
,把x=1,y=0代入,解得![]() .
.
∴直线M1N1的函数表达式为![]() ;
;
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴N1M1∥M2N2,N1M1=M2N2.
∴线段M2N2与线段N1M1关于原点O成中心对称.
∴M2点坐标为(-1,0),N2点坐标为(0,-1).
设直线M2N2的函数表达式为![]() ,把x=-1,y=0代入,解得
,把x=-1,y=0代入,解得![]() ,
,
∴直线M2N2的函数表达式为![]()
所以,直线MN的函数表达式为![]() 或
或![]() .
.

【题目】受气候的影响,某超市蔬菜供应紧张,需每天从外地调运蔬菜1000斤.超市决定从甲、乙两大型蔬菜棚调运蔬菜,已知甲蔬菜棚每天最多可调出800斤,乙蔬菜棚每天最多可调运600斤,从两蔬菜棚调运蔬菜到超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲蔬菜棚 | 120 | 0.03 |
乙蔬菜棚 | 80 | 0.05 |
(1)若某天调运蔬菜的总运费为3840元,则从甲、乙两蔬菜棚各调运了多少斤蔬菜?
(2)设从甲蔬菜棚调运蔬菜![]() 斤,总运费为
斤,总运费为![]() 元,试写出
元,试写出![]() 与
与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?