Question

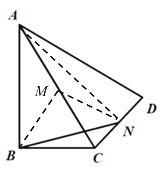
【题目】如图，在Rt△ABC中，∠ABC＝90°，∠BAC=32°，斜边AC＝6，将斜边AC绕点A逆时针方向旋转26°到达AD的位置，连接CD，取线段CD的中点N，连接BN，则BN的长为_________．

Answer 1

【答案】

【解析】

设M为AC中点，连接AN，BM，MN，根据直角三角形斜边中点定理得出MB=MN=，同时算出∠BMN=90°，最后利用勾股定理算出BN的长.

解：设M为AC中点，连接AN，BM，MN，

由旋转可知：AC=AD=6，∠CAD=26°，

∵∠BAC=32°，∠ABC=90°，

∴∠ACB=58°，

∵AC=AD，N为CD中点，M为AC中点，

∴MB=MC=MN=3，

∴∠MBC=∠MCB=58°，∠MCN=∠MNC=（180-26）÷2=77°，

∴∠BMC=64°，∠CMN=26°，

∴∠BMN=90°，即△BMN为等腰直角三角形，

∴BN=.

故答案为：.