题目内容
【题目】如图,在正方形ABCD中,AB=![]() ,E是对角线AC上的动点,以DE为边作正方形DEFG,H是CD的中点,连接GH,则GH的最小值为____.
,E是对角线AC上的动点,以DE为边作正方形DEFG,H是CD的中点,连接GH,则GH的最小值为____.

【答案】![]()
【解析】
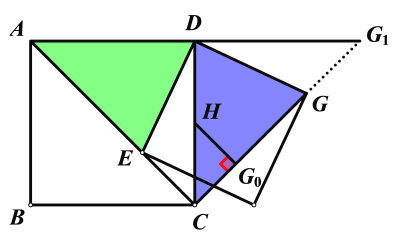
由∠ADC=∠EDG=90°,推出∠ADE=∠CDG,连接GC,容易证明△DAE≌△DCG,推出AE=CG,当E点位于C点时,G点位于AD的延长线G1处,进而推出G点在CG1这条线段上运动,再由点到直线的距离垂线段最短知,过H向CG1作垂线,得到GH的最小值.
解:连接CG,如下图所示:
∵∠ADC=∠EDG=90°
∴∠ADC-∠EDC=∠EDG-∠EDC
∴∠ADE=∠CDG
在△ADE和△CDG中
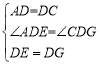 ,∴△ADE和△CDG(SAS)
,∴△ADE和△CDG(SAS)
∴AE=CG
当E点位于C点时,G点位于G1处
当E但位于A点时,G点位于C处,
故E点在AC上运动时,G点在CG1上运动
故由点到直线的距离垂线段最短可知:
过H点作HG0⊥CG时,此时HG0最小
又H是CD的中点,∴CH=![]() CD=
CD=![]()
又∠DCG=45°,
∴HG0=![]() CH=
CH=![]() .
.
故答案为:![]()

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目