题目内容
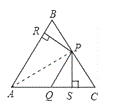
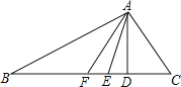
【题目】 如图,AD,AE和AF分别是△ABC的高、角平分线和中线.
(1)对于下面的五个结论:①BC=2BF;②∠CAE=![]() ∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△ADC.其中错误的是______(只填序号);
∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△ADC.其中错误的是______(只填序号);
(2)若∠C=70°,∠ABC=28°,求∠DAE的度数.
【答案】(1)③⑤;(2)21°。
【解析】
(1)根据三角形的高、角平分线和中线的定义即可得到AD⊥BC,∠CAE=![]() ∠CAB,BC=2BF,S△AFB=S△AFC,无法确定AE=BE,S△AFB=S△ADC.
∠CAB,BC=2BF,S△AFB=S△AFC,无法确定AE=BE,S△AFB=S△ADC.
(2)先根据三角形内角和得到∠CAB=180°-∠ABC-∠C=82°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=41°,∠ADC=90°,则∠DAC=90°-∠C=20°,然后利用∠DAE=∠CAE-∠DAC计算即可.
∠CAB=41°,∠ADC=90°,则∠DAC=90°-∠C=20°,然后利用∠DAE=∠CAE-∠DAC计算即可.
(1)∵AD,AE和AF分别是△ABC的高、角平分线和中线,
∴AD⊥BC,∠CAE=∠BAE=![]() ∠CAB,BF=CF,BC=2BF,
∠CAB,BF=CF,BC=2BF,
∵S△AFB=![]() BFAD,S△AFC=
BFAD,S△AFC=![]() CFAD,
CFAD,
∴S△AFB=S△AFC,故①②④正确,
∵BF=CF,
∴BE>CE,
∵BF>CD,
∴S△AFB>S△ADC.故③⑤错误,
故答案为③⑤.
(2)∵∠C=70°,∠ABC=28°,
∴∠CAB=180°-∠ABC-∠C=82°,
∴∠CAE=![]() ∠CAB=41°,
∠CAB=41°,
∵∠ADC=90°,∠C=70°,
∴∠DAC=20°
∴∠DAE=∠CAE-∠DAC=41°-20°=21°.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
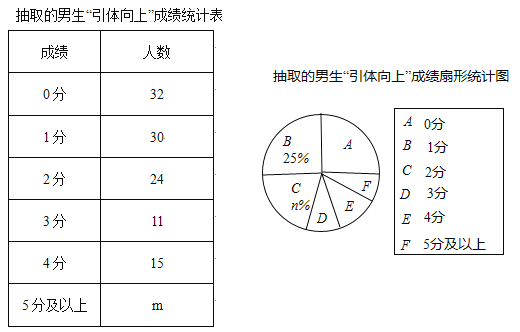
金博士一点全通系列答案【题目】为了确定射击比赛的选手,调取了甲、乙两人在5次打靶测试中的成绩(单位:环)如下:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲 | 7 | 8 | 8 | 8 | 9 |
乙 | 7 | 7 | 7 | 9 | 10 |
(1)根据以上数据填写下表:
平均数/环 | 众数/环 | 中位数/环 | 方差 | |
甲 | 8 | 8 | 0.4 | |
乙 | 7 |
(2)从统计的角度教练选择谁参加射击比赛更合适,其理由是什么?
(3)若再射击l次,且命中8环,则其射击成绩的方差_______.(填“变大”“变小”或“不变”)