题目内容
【题目】若一组数据x1，x2，x3，x4，…xn，的方差为5，则另一组数据2x1+3，2x2+3，2x3+3，2x4+3，…2xn+3的方差为_____．
【答案】20
【解析】
首先我们要清楚把一组数据的每一个数据同时扩大相同的倍数时对平均数和方差的影响，每一个数据都同时加上一个数时对平均数和方差的影响.然后进行判断数据变化后的方差.
假设
的平均数是a，方差为b
则有
①当每一个数据同时扩大m倍数时：
此时平均数为:
此时方差为：
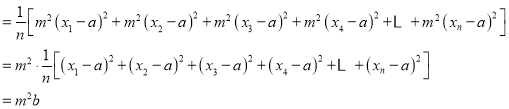
故可得出结论为：每一个数据同时扩大m倍数时，平均数扩大m倍，方差扩大
倍.
②每一个数据都同时增加m时：
此时平均数为:
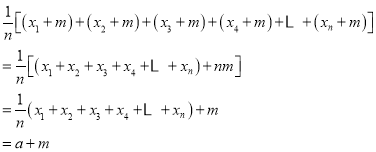
此时方差为：
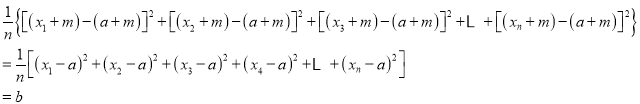故可得出结论为：每一个数据同时增加m时，平均数增加m，方差不变.
根据以上结论：
2x1+3，2x2+3，2x3+3，2x4+3，…2xn+3是由x1，x2，x3，x4，…xn 每个数据扩大2倍再增加3得到，扩大两倍则方差扩大
倍，再加多少对方差没影响.
所以2x1+3，2x2+3，2x3+3，2x4+3，…2xn+3的方差为4×5=20
故答案为：20.
练习册系列答案
相关题目
