Question

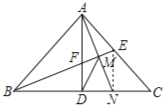
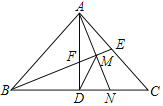
【题目】如图，等腰Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，AM的延长线交BC于点N，连接DM，下列结论：①AE＝AF；②DF＝DN；③AN＝BF；④EN⊥NC；⑤AE＝NC，其中正确结论的个数是（　　）

A. 2个B. 3个C. 4个D. 5个

Answer 1

【答案】D

【解析】

①根据等腰直角三角形的性质及角平分线的定义求得，继而可得∠AFE=∠AEB=67.5°，即可判断①；

②求出BD=AD，∠DBF=∠DAN，∠BDF=∠ADN，证△DFB≌△DAN，即可判断②；

③根据A、B、D、M四点共圆求出∠ADM=22.5°，根据三角形外角性质求出∠DNM，求出∠MDN=∠DNM，即可判断③；

④求出∠BMD=45°=∠BMN，即可判断④；

⑤证明△AFB≌△CNA可得AF=CN，由AF=AE，即可判断⑤．

解：∵等腰Rt△ABC中，∠BAC＝90°，AD⊥BC，

∴∠BAD＝∠CAD＝∠C＝45°，

∵∵BE平分∠ABC，

∴∠ABE＝∠CBE＝∠ABC＝22.5°，

∴∠AEF＝∠CBE+∠C＝22.5°+45°＝67.5°，∠AFE＝∠FBA+∠BAF＝22.5°+45°＝67.5°

∴∠AEF＝∠AFE，

∴AE＝AF，

故①正确；

∵∠BAC＝90°，AC＝AB，AD⊥BC，

∴∠ABC＝∠C＝45°，AD＝BD＝CD，∠ADN＝∠ADB＝90°，

∴∠BAD＝45°＝∠CAD，

∵BE平分∠ABC，

∴∠ABE＝∠CBE＝∠ABC＝22.5°，

∴∠BFD＝∠AEB＝90°﹣22.5°＝67.5°，

∴AFE＝∠BFD＝∠AEB＝67.5°，

∴AF＝AE，AM⊥BE，

∴∠AMF＝∠AME＝90°，

∴∠DAN＝90°﹣67.5°＝22.5°＝∠MBN，

在△FBD和△NAD中

，

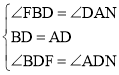∴△FBD≌△NAD（ASA），

∴DF＝DN，AN＝BF，

∴②③正确；

连接EN，

∵AE＝AF，FM＝EM，

∴AM⊥EF，

∴∠BMA＝∠BMN＝90°，

∵BM＝BM，∠MBA＝∠MBN，

∴△MBA≌△MBN，

∴AM＝MN，

∴BE垂直平分线段AN，

∴AB＝BN，EA＝EN，

∵BE＝BE，

∴△ABE≌△NBE，

∴∠ENB＝∠EAB＝90°，

∴EN⊥NC．

故④正确；

在△AFB和△CNA中，

，

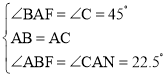∴△AFB≌△CAN（ASA），

∴AF＝CN，

∵AF＝AE，

∴AE＝CN，

故⑤正确；

其中正确结论的个数是：①②③④⑤，共5个；

故选：D．