题目内容
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
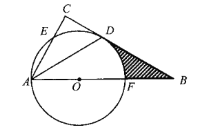
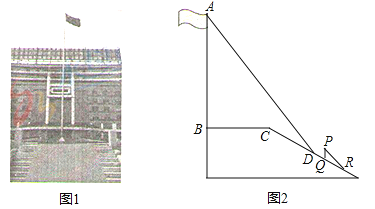
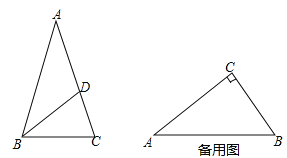
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
【答案】(1)1;(2)证明见解析;(3)EF的长是![]() .
.
【解析】试题分析:(1)过等边三角形的内心分别作三边的平行线,即可得出答案;
(2)由等腰三角形的性质得出∠ABC=∠C=∠BDC,证出△BCD∽△ABC即可;
(3)分两种情况:①当![]() 时,EF∥AB,由勾股定理求出AB=
时,EF∥AB,由勾股定理求出AB=![]() =5,作DN⊥BC于N,则DN∥AC,DN是Rt△ABC的内切圆半径,求出DN=
=5,作DN⊥BC于N,则DN∥AC,DN是Rt△ABC的内切圆半径,求出DN=![]() (AC+BC-AB)=1,由几啊平分线定理得出
(AC+BC-AB)=1,由几啊平分线定理得出![]() ,求出CE=
,求出CE=![]() ,证明△CEF∽△CAB,得出对应边成比例求出EF=
,证明△CEF∽△CAB,得出对应边成比例求出EF=![]() ;
;
②当![]() 时,同理得:EF=
时,同理得:EF=![]() 即可.
即可.
试题解析:(1)等边三角形“內似线”的条数为3条;理由如下:
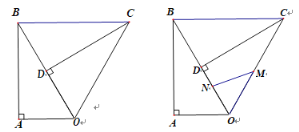
过等边三角形的内心分别作三边的平行线,如图1所示:
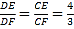
则△AMN∽△ABC,△CEF∽△CBA,△BGH∽△BAC,
∴MN、EF、GH是等边三角形ABC的內似线”;
(2)∵AB=AC,BD=BC,
∴∠ABC=∠C=∠BDC,
∴△BCD∽△ABC,
∴BD是△ABC的“內似线”;
(3)设D是△ABC的内心,连接CD,

则CD平分∠ACB,
∵EF是△ABC的“內似线”,
∴△CEF与△ABC相似;
分两种情况:①当![]() 时,EF∥AB,
时,EF∥AB,
∵∠ACB=90°,AC=4,BC=3,
∴AB=![]() =5,
=5,
作DN⊥BC于N,如图2所示:
则DN∥AC,DN是Rt△ABC的内切圆半径,
∴DN=![]() (AC+BC-AB)=1,
(AC+BC-AB)=1,
∵CD平分∠ACB,
∴![]() ,
,
∵DN∥AC,
∴![]() ,即
,即![]() ,
,
∴CE=![]() ,
,
∵EF∥AB,
∴△CEF∽△CAB,
∴![]() ,即
,即 ,
,
解得:EF=![]() ;
;
②当![]() 时,同理得:EF=
时,同理得:EF=![]() ;
;
综上所述,EF的长为![]() .
.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案