Question

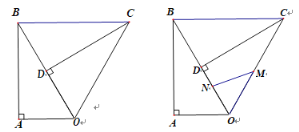
【题目】已知Rt△OAB，OAB90，ABO30，斜边OB4，将Rt△OAB绕点O顺时针旋转60，得到△COD，如图1，连接BC．

（1）求BC的长度；

（2）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿OCB路径匀速运动，N沿OBC路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5个单位/秒，点N的运动速度为1个单位/秒，设运动时间为x秒，△OMN的面积为y，求y关于x的函数解析式，并直接写出自变量x的取值范围．

Answer 1

【答案】（1）4；（2）

【解析】

（1）只要证明△OBC是等边三角形即可．
（2）分三种情形讨论求解即可解决问题：①当0＜x≤时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E．②当＜x≤4时，M在BC上运动，N在OB上运动．③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G．

（1）解：∵，，

∴．

∴．

∵，

∴．

∴．

∴．

∵，

∴．

（2）①当时，作于．

∵，

∴．

∴．

∴．

∴．

②当时，作于．

由（1）得，为等边三角形，

∴．

∴．

∴．

．

③当时，作于．

∵，∴．

∴．

．

综上所述，.