题目内容
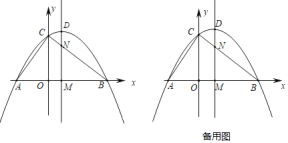
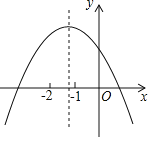
【题目】已知二次函数y＝ax2+bx+c的图象如图所示，下列结论：①ac＜0，②b﹣2a＜0，③b2﹣4ac＜0，④a﹣b+c＜0，正确的是( )
A.①②B.①④C.②③D.②④
【答案】A
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所给结论进行判断．
①图象开口向下，与y轴交于正半轴，能得到：a＜0，c＞0，
∴ac＜0，故①正确；
②∵对称轴x＜﹣1，
∴
＜﹣1，-2a＞0，
∴b＜2a，
∴b﹣2a＜0，故②正确；
③图象与x轴有2个不同的交点，依据根的判别式可知b2﹣4ac＞0，故③错误；
④当x＝﹣1时，y＞0，∴a﹣b+c＞0，故④错误，
故选A．
练习册系列答案
相关题目
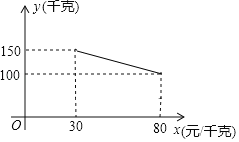
【题目】某商场试销一种成本为每件
元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于
，经试销发现，销售量
（件）与销售单价
（元）符合一次函数，所调查的部分数据如表：
销售单价 | 60 | 65 | 70 |
|
销售量 | 60 | 55 | 50 |
|
（1）求出与之间的函数表达式；
（2）若该商场获得利润为
元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少？
（3）销售单价定为多少元时，该商场获得的利润恰为
元？
