题目内容
如图:在平行四边形ABCD中, AB:AD =3:2, ∠ADB=60º,那么 A的值等于
A的值等于

 A的值等于
A的值等于
A. | B. | C. | D. |
A
作出辅助线,构造直角三角形,运用三角形面积相等,求出三角形的高,然后运用sin2α+cos2α=1,根据题中所给的条件,在直角三角形中解题,由角的余弦值与三角形边的关系求解.
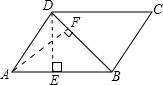
解:作AF⊥DB于F,作DE⊥AB于E.
设DF=x,
∵∠ADB=60°,∠AFD=90°,
∴∠DAF=30°,
则AD=2x,
∴AF=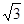 x,
x,
又∵AB:AD=3:2,
∴AB=3x,于是BF=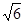 x,
x,
∴3x?DE=(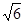 +1)x?
+1)x?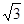 x,
x,
DE=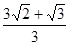 x,sin∠A=
x,sin∠A=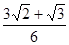 ,
,
cos∠A=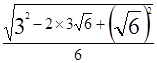 =
=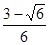 .
.
故选A.
本题考查了解直角三角形、平行四边形的性质.解题时,利用了三角函数的定义及三角形面积公式.

解:作AF⊥DB于F,作DE⊥AB于E.
设DF=x,
∵∠ADB=60°,∠AFD=90°,
∴∠DAF=30°,
则AD=2x,
∴AF=
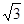 x,
x,又∵AB:AD=3:2,
∴AB=3x,于是BF=
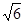 x,
x,∴3x?DE=(
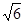 +1)x?
+1)x?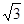 x,
x,DE=
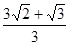 x,sin∠A=
x,sin∠A=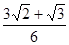 ,
,cos∠A=
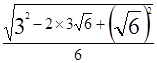 =
=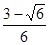 .
.故选A.
本题考查了解直角三角形、平行四边形的性质.解题时,利用了三角函数的定义及三角形面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
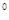 和 10
和 10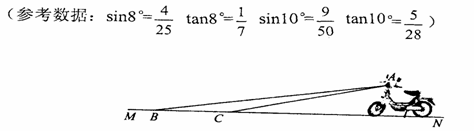
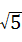 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )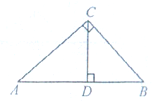
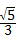 B、
B、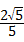
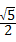 D、
D、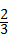


 tan30°-tan45°
tan30°-tan45°

 ,AE=
,AE= ,
,



 45°+
45°+ ×
× -tan
-tan