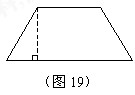
题目内容
已知:如图,等边△ABC中,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.

(1)猜想:线段AE、MD之间有怎样的数量关系,并加以证明;
(2)在(1)的条件下延长BM到P,使MP=BM,连接CP,若AB=7 ,AE=
,AE= ,
,
求tan∠BCP的值.

(1)猜想:线段AE、MD之间有怎样的数量关系,并加以证明;
(2)在(1)的条件下延长BM到P,使MP=BM,连接CP,若AB=7
 ,AE=
,AE= ,
,求tan∠BCP的值.
(1)猜想: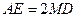 --------------------------------------
-------------------------------------- ----1分
----1分
证明:∵ △ABC是等边三角形,点D为BC边的中点,
∴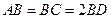
∵ ∠BAE=∠BDF , ∠ABE=∠DBM
∴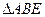 ∽
∽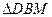 ----------------------2分
----------------------2分
∴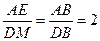 即
即 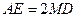 -------------3分
-------------3分
(2)解:如图, 连接EP
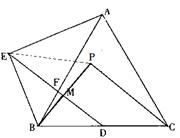
由(1)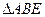 ∽
∽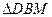
∴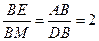
∴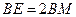
 ∵
∵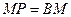
∴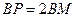
∴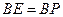
∵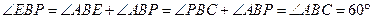
∴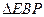 为等边三角形 ----------------------4分
为等边三角形 ----------------------4分
∴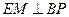
∴
∴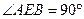 -----------------------5分
-----------------------5分
在Rt△AEB中,AB=7,AE=
∴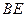 =
=
∴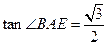 -------------------6分
-------------------6分
∵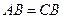 ,
,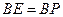 ,∠ABE=∠DBM
,∠ABE=∠DBM
∴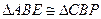
∴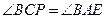
∴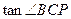 =
=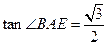 ---------7分
---------7分
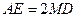 --------------------------------------
-------------------------------------- ----1分
----1分证明:∵ △ABC是等边三角形,点D为BC边的中点,
∴
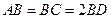
∵ ∠BAE=∠BDF , ∠ABE=∠DBM
∴
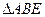 ∽
∽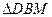 ----------------------2分
----------------------2分∴
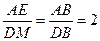 即
即 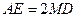 -------------3分
-------------3分(2)解:如图, 连接EP

由(1)
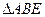 ∽
∽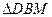
∴
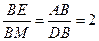
∴
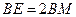
 ∵
∵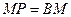
∴
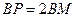
∴
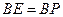
∵
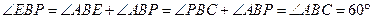
∴
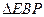 为等边三角形 ----------------------4分
为等边三角形 ----------------------4分∴
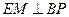
∴

∴
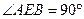 -----------------------5分
-----------------------5分在Rt△AEB中,AB=7,AE=

∴
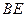 =
=
∴
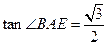 -------------------6分
-------------------6分∵
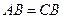 ,
,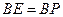 ,∠ABE=∠DBM
,∠ABE=∠DBM∴
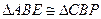
∴
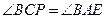
∴
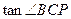 =
=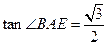 ---------7分
---------7分略

练习册系列答案
相关题目
 ∥AB,F是
∥AB,F是 A的值等于
A的值等于




 , tan∠BCE=
, tan∠BCE= ,那么CE=
,那么CE= 
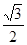 ,则α= 。
,则α= 。