Question

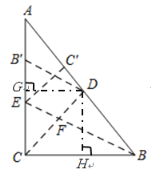
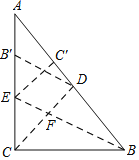
【题目】如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝4，沿CD折叠，使点B落在CA边上的B′处，展开后，再沿BE折叠，使点C落在BA边上的C′处，CD与BE交于点F．

（1）求AC′的长度；

（2）求CE的长度；

（3）比较四边形EC′DF与△BCF面积的大小，并说明理由．

Answer 1

【答案】（1）2；（2）；（3）S四边形EC′DF＜S△BCF，理由详见解析．

【解析】

（1）由勾股定理得出AB的长度，根据翻折可知BC＝BC′，即可求AC′的长度；

（2）设CE的长为x，根据翻折可得EC′＝EC，则AE=4-x，在Rt△AC′E中根据勾股定理即可求C′E的长度；

（3）过点D分别作DG⊥AC于G，DH⊥BC于H，根据翻折可得CD为∠ACB的角平分线，得出DG=DH，然后由面积法求得DH的长，再求得△BDC和△BEC′的面积，由S△BDC＝S△BFC+S△BDF，S△BEC′＝S四边形EC′DF+S△BDF，进而可以比较四边形EC′DF与△BCF面积的大小．

解：（1）∵∠ACB＝90°，BC＝3，AC＝4，

∴AB=，

根据翻折可知：BC＝BC′＝3，

∴AC′＝AB﹣BC′＝5﹣3＝2；

（2）由折叠的性质可得：

∠BC′E＝∠BCE＝90°=∠AC′E=90°，CE=CE′，

设CE=x，则C′E=x，AE=4-x，

在Rt△AC′E中，由勾股定理得，

x2+22=(4-x)2，解得x=．

即CE的长度为；

（3）结论：S四边形EC′DF＜S△BCF，理由如下：

过点D分别作DG⊥AC于G，DH⊥BC于H，

由折叠得，CD为∠ACB的角平分线，∴DG=DH，

∵S△ABC=S△ACD+S△BCD，∴×AC×BC=×AC×DG+×BC×DH，

∴3×4=3×DH+4×DH，∴DH=．

∴S△BDC＝BCDH＝3×＝，S△BEC′＝S△BEC＝BCCE＝×3×＝，

∵＞，∴S△BDC＞S△BEC′，

∵S△BDC＝S△BFC+S△BDF，S△BEC′＝S四边形EC′DF+S△BDF，

∴S四边形EC′DF＜S△BCF．