题目内容
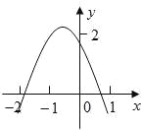
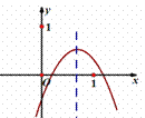
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列代数式:①ac;②a+b+c;③4a-2b+c;④2a+b;⑤b2-4ac中,值大于0的序号为______________.
【答案】①②⑤
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线与y轴的交点在x轴的下方,
∴c<0,
∴ac>0,故①正确;
当x=1时,y<0,即a+b+c<0,故②错误;
当x=﹣2时,y<0,即4a-2b+c<0,故③错误;
对称轴为x=![]() <1,a<0,
<1,a<0,
∴-b>2a,
∴2a+b<0,故④错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,故⑤正确.
故答案为:①②⑤.

练习册系列答案
相关题目
【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.