题目内容
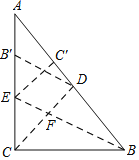
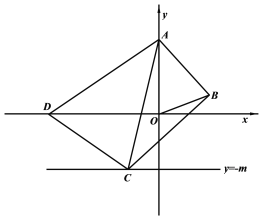
【题目】已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线![]() 于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD.
(2)设△ACD的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)若四边形ABCD恰有一组对边平行,求![]() 的值.
的值.
【答案】(1)证明详见解析;(2)S=![]() (m+1)2+
(m+1)2+![]() (m>
(m>![]() );(3)3或8.
);(3)3或8.
【解析】
试题(1)利用两点间的距离公式计算出AB=5,则AB=OA,则可根据“HL”证明△ABC≌△AOD;
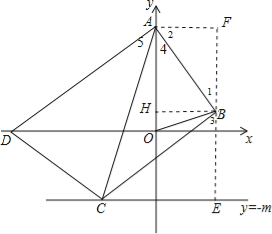
(2)过点B作直线BE⊥直线y=﹣m于E,作AF⊥BE于F,如图,证明Rt△ABF∽Rt△BCE,利用相似比可得BC=![]() (m+1),再在Rt△ACB中,由勾股定理得AC2=AB2+BC2=25+
(m+1),再在Rt△ACB中,由勾股定理得AC2=AB2+BC2=25+![]() (m+1)2,然后证明△AOB∽△ACD,利用相似的性质得
(m+1)2,然后证明△AOB∽△ACD,利用相似的性质得![]() ,而S△AOB=
,而S△AOB=![]() ,于是可得S=
,于是可得S=![]() (m+1)2+
(m+1)2+![]() (m>
(m>![]() );
);
(3)作BH⊥y轴于H,如图,分类讨论:当AB∥CD时,则∠ACD=∠CAB,由△AOB∽△ACD得∠ACD=∠AOB,所以∠CAB=∠AOB,利用三角函数得到tan∠AOB=3,tan∠ACB=![]() ,所以
,所以![]() =3;当AD∥BC,则∠5=∠ACB,由△AOB∽△ACD得到∠4=∠5,则∠ACB=∠4,根据三角函数定义得到tan∠4=
=3;当AD∥BC,则∠5=∠ACB,由△AOB∽△ACD得到∠4=∠5,则∠ACB=∠4,根据三角函数定义得到tan∠4=![]() ,tan∠ACB=
,tan∠ACB=![]() ,则
,则![]() =
=![]() ,然后分别解关于m的方程即可得到m的值.
,然后分别解关于m的方程即可得到m的值.
试题解析:(1)证明:∵A(0,5),B(3,1),
∴AB=![]() =5,
=5,
∴AB=OA,
∵AB⊥BC,
∴∠ABC=90°,
在Rt△ABC和Rt△AOD中,
![]() ,
,
∴Rt△ABC≌Rt△AOD;
(2)解:过点B作直线BE⊥直线y=﹣m于E,作AF⊥BE于F,如图,∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∴Rt△ABF∽Rt△BCE,
∴![]() ,即
,即![]() ,
,
∴BC=![]() (m+1),
(m+1),
在Rt△ACB中,AC2=AB2+BC2=25+![]() (m+1)2,
(m+1)2,
∵△ABC≌△AOD,
∴∠BAC=∠OAD,即∠4+∠OAC=∠OAC+∠5,
∴∠4=∠5,
而AO=AB,AD=AC,
∴△AOB∽△ACD,
∴![]() =
=![]() ,
,
而S△AOB=![]() ×5×3=
×5×3=![]() ,
,
∴S=![]() (m+1)2+
(m+1)2+![]() (m>
(m>![]() );
);
(3)作BH⊥y轴于H,如图,
当AB∥CD时,则∠ACD=∠CAB,
而△AOB∽△ACD,
∴∠ACD=∠AOB,
∴∠CAB=∠AOB,
而tan∠AOB=![]() =3,tan∠ACB=
=3,tan∠ACB=![]() =
=![]() =
=![]() ,
,
∴![]() =3,解得m=8;
=3,解得m=8;
当AD∥BC,则∠5=∠ACB,
而△AOB∽△ACD,
∴∠4=∠5,
∴∠ACB=∠4,
而tan∠4=![]() ,tan∠ACB=
,tan∠ACB=![]() ,
,
∴![]() =
=![]() ,
,
解得m=3.
综上所述,m的值为3或8.

 阅读快车系列答案
阅读快车系列答案