题目内容
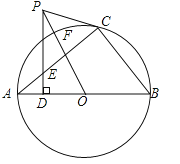
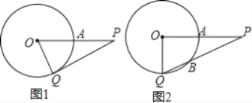
【题目】已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
【答案】(1) ∠QOP=60°; (2) QB=![]() .
.
【解析】
(1)先利用切线的性质得到OQ⊥PQ,然后利用锐角三角函数值的定义求∠QOP的大小;
(2)利用垂径定理,作OD⊥BQ于D,如图2,则QD=BD,先利用勾股定理计算出PQ,再证明Rt△QOD∽Rt△QPO,利用相似比计算出QD,从而得到BQ的长.
(1)如图1,∵PQ是⊙O的切线,∴OQ⊥PQ,∵A是OP的中点,∴OP=2OA,
在Rt△OPQ中,cos∠QOP=![]() =
=![]() ,∴∠QOP=60°;
,∴∠QOP=60°;
(2)作OD⊥BQ于D,如图2,则QD=BD,∵∠QOP=90°,OP=4,OQ=2,∴PQ=2![]() ,
,
∵∠OQD=∠PQO,∴Rt△QOD∽Rt△QPO,∴QD:OQ=OQ:QP,即QD:2=2:2![]() ,
,
∴QD=![]() ,∴QB=2QD=
,∴QB=2QD=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.