题目内容
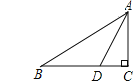
【题目】Rt△ABC中,∠C=90°,AC=![]() ,点D为BC边上一点,且BD=AD,∠ADC=60°,则△ABC的周长为_____.(结果保留根号)
,点D为BC边上一点,且BD=AD,∠ADC=60°,则△ABC的周长为_____.(结果保留根号)
【答案】3![]() +3.
+3.
【解析】
要求△ABC的周长,只要求得BC及AB的长度即可.在Rt△ADC中,∠ADC=60°可得∠DAC=30°,可得CD=![]() AD,再根据勾股定理可以求得AD,CD的长度,继而求得BC的长度,最后运用勾股定理可以求得AB的长度,得出△ABC的周长.
AD,再根据勾股定理可以求得AD,CD的长度,继而求得BC的长度,最后运用勾股定理可以求得AB的长度,得出△ABC的周长.
解:在Rt△ADC中,∠C=90°,∠ADC=60°,
∴∠DAC=30°,∴CD=![]() AD,
AD,
根据勾股定理可得,AD2=CD2+AC2,
∴4CD2=CD2+3,∴CD=1,AD=2,
∴BC=BD+DC=AD+DC=3.
在Rt△ABC中,AB=![]() =2
=2![]() ,
,
∴△ABC的周长=AB+BC+AC=2![]() +3+
+3+![]() =3
=3![]() +3.
+3.
故答案为:3![]() +3.
+3.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目