题目内容
【题目】如图,四边形ABCD为矩形,点E是边BC的中点,AF∥ED,AE∥DF
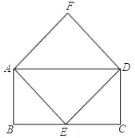
(1)求证:四边形AEDF为菱形;
(2)试探究:当AB:BC= ,菱形AEDF为正方形?请说明理由.
【答案】(1)见解析;(2)当AB:BC=1:2,菱形AEDF为正方形.理由见解析.
【解析】
(1)先证明四边形AEDF为平行四边形,再证明△ABE≌△DCE得到EA=ED,从而可判断四边形AEDF为菱形;
(2)当AB:BC=1:2,则AB=BE,于是可判断△ABE为等腰直角三角形,则∠AEB=45°,利用△ABE≌△DCE得到∠DEC=45°,所以∠AED=90°,根据根据正方形的判定方法可判断菱形AEDF为正方形.
(1)证明:∵AF∥ED,AE∥DF,
∴四边形AEDF为平行四边形,
∵四边形ABCD为矩形,
∴AB=CD,∠B=∠C=90°,
∵点E是边BC的中点,
∴BE=CE,
在△ABE和△DCE中
 ,
,
∴△ABE≌△DCE,
∴EA=ED,
∴四边形AEDF为菱形;
(2)解:当AB:BC=1:2,菱形AEDF为正方形.
理由如下:
∵AB:BC=1:2,
而点E是边BC的中点,
∴AB=BE,
∴△ABE为等腰直角三角形,
∴∠AEB=45°,
∵△ABE≌△DCE,
∴∠DEC=45°,
∴∠AED=90°,
∵四边形AEDF为菱形,
∴菱形AEDF为正方形.
故答案为1:2.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目