题目内容
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了![]() 层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]()
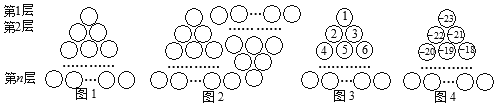
如果图中的圆圈共有13层,请解决下列问题:
(1)若自上往下,在图①每个圆圈中填上一串连续的正整数1,2,3,4,…,得到图3,写出第11层最左边这个圆圈中的数;
(2)若自上往下,在图①每个圆圈中填上一串连续的整数-23,-22,-21,20,…,得到图4,写出第10层最右边圆圈内的数;
(3)根据以上规律,求图4中第1层到第10层所有圆圈中各数之和(写出计算过程).
【答案】(1)56;(2)31;(3)220.
【解析】
(1)由第11层最左边这个圆圈中的数是第10层的最后一个数加1,根据公式计算出10层的圆圈数即可得答案;(2)由(1)可知10层的圆圈数,根据第一层的数字即可求出第10层最右边圆圈内的数;(3)利用(2)把所有数相加即可.
(1)∵第11层最左边这个圆圈中的数是第10层的最后一个数加1,
∴第11层最左边这个圆圈中的数是![]() +1=56.
+1=56.
(2)由(1)得10层共有![]() =55个圆圈,
=55个圆圈,
∵第一个圆圈的数字是-23,
∴第10层最右边圆圈内的数是-23+55-1=31.
(3)图4中10层共有55个数,其中23个负数,1个0,31个正数,
所以图4中所有圆圈中各数的和为:-(1+2+3+4+…+23)+(1+2+3+4+…+31)=220.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目