Question

【题目】“六一”前夕，某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套，并且购进的三种玩具都不少于10套，设购进A种玩具x套，B种玩具y套，三种电动玩具的进价和售价如表所示

型 号	A	B	C
进价（元/套）	40	55	50
售价（元/套）	50	80	65

（1）用含x、y的代数式表示购进C种玩具的套数；

（2）求y与x之间的函数关系式；

（3）假设所购进的这三种玩具能全部卖出，且在购销这种玩具的过程中需要另外支出各种费用200元．

①求出利润P（元）与x（套）之间的函数关系式；②求出利润的最大值，并写出此时三种玩具各多少套．

Answer 1

【答案】当x取最大值23时，P有最大值，最大值为595元．此时购进A、B、C种玩具分别为23套、16套、11套．

【解析】试题分析：

（1）利用三种玩具的总和是50套可求解；

（2）结合总费用是2350列方程可得y与x之间的函数关系式；

（3）①根据利润=销售收入﹣进价﹣其它费用列出p与x之间的函数关系式；

②根据题意确定自变量x的取值范围，由一次函数的性质可得到最大值，从而求解.

解：（1）已知共购进A、B、C三种新型的电动玩具共50套，故购进C种玩具套数为：50﹣x﹣y；

（2）由题意得40x+55y+50（50﹣x﹣y）=2350，整理得y=2x﹣30；

（3）①利润=销售收入﹣进价﹣其它费用，

故：p=（50﹣40）x+（80﹣55）y+（65﹣50）（50﹣x﹣y）﹣200，

又∵y=2x﹣30，

∴整理得p=15x+250，

②购进C种电动玩具的套数为：50﹣x﹣y=50﹣x﹣（2x﹣30）=80﹣3x，

据题意列不等式组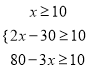，解得20≤x≤，

∴x的范围为20≤x≤，且x为整数，故x的最大值是23，

∵在p=15x+250中，k=15＞0，

∴P随x的增大而增大，

∴当x取最大值23时，P有最大值，最大值为595元．此时购进A、B、C种玩具分别为23套、16套、11套．