题目内容
【题目】如图,直线AB,CD被直线BD,DF所截,AB∥CD,BFBD,垂足为B,EG平分BED,CDE50,F25.
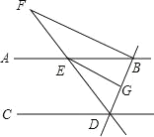
⑴求证:EG∥BF;⑵求BDC的度数.
【答案】(1) 见详解;(2)115°.
【解析】
(1)根据平行线的性质得到∠BED=∠CDE=50°,由角平分线的定义得到∠DEQ=25°,然后根据平行线的性质即可得到结论;
(2)由(1)得∠FBE=∠BFG=25°,根据平行线的性质即可得到结论.
解:(1)∵AB∥CD,∠CDE=50°,
∴∠BED=∠CDE=50°,
∵EG平分∠DEB,
∴∠DEQ=25°,
∵∠F=25°,
∴BF∥EG,
∵FB⊥BD,
∴EG⊥BD;
(2)由(1)得∠FBE=∠BFG=25°,
∵∠FBD=90°,
∴∠EBD=65°,
∵AB∥CD,
∴∠CDB=115°.

练习册系列答案
相关题目
【题目】“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如表所示
型 号 | A | B | C |
进价(元/套) | 40 | 55 | 50 |
售价(元/套) | 50 | 80 | 65 |
(1)用含x、y的代数式表示购进C种玩具的套数;
(2)求y与x之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.