题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.

(1)求证:DF是⊙O的切线;
(2)若CF=2,DF=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析(2)8![]() ﹣
﹣![]() π
π
【解析】(1)连接AD、OD,由AB为直径可得出点D为BC的中点,由此得出OD为△BAC的中位线,再根据中位线的性质即可得出OD⊥DF,从而证出DF是⊙O的切线;
(2)CF=1,DF=![]() ,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
(1)证明:连接AD、OD,如图所示.
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,∵AC=AB,
∴点D为线段BC的中点.
∵点O为AB的中点,
∴OD为△BAC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线.
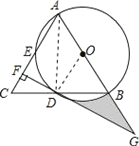
(2)解:在Rt△CFD中,CF=2,DF=2![]() ,
,
∴tan∠C=![]() =
=![]() ,CD=4,
,CD=4,
∴∠C=60°,
∵AC=AB,
∴△ABC为等边三角形,
∴AB=8.
∵OD∥AC,
∴∠DOG=∠BAC=60°,
∴DG=ODtan∠DOG=4![]() ,
,
∴S阴影=S△ODG﹣S扇形OBD=![]() DGOD﹣
DGOD﹣![]() πOB2=8
πOB2=8![]() ﹣
﹣![]() π
π

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目




