Question

【题目】如图，在矩形中，，动点从点出发，沿射线以每秒个单位的速度向点方向运动，连接，把沿翻折，得到．设点的运动时间为．

（1）若，当三点在同一直线上时，求的值；

（2）若点到直线的距离等于，求的值；

（3）若的最小值为，直接写出的值．

Answer 1

【答案】（1）t=3 -；（2）t= ；（3）m= ．

【解析】

（1）如图1中，设PD=t．则PA=3-t．首先证明BP=BC=6，在Rt△ABP中利用勾股定理即可解决问题；

（2）通过添加辅助线，构造直角三角形再解决问题；

（3）当点A,点E，点C在同一条直线上时，AE最短，利用勾股定理求值即可．

解：（1）如图1中，设PD=t．则PA=3-t

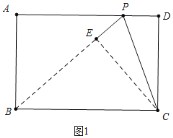
∵P、B、E共线，
∴∠BPC=∠DPC，
∵AD∥BC，
∴∠DPC=∠PCB，
∴∠BPC=∠PCB，
∴BP=BC=3，
在Rt△ABP中，

∵AB2+AP2=BP2，
∴22+（3-t）2=32，
∴t=3 +（舍去）或3-

∴当t=3 -时，三点在同一直线上．

（2） 过点E作MN⊥BC，交AD于点M

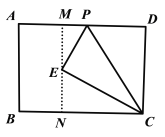
∵四边形ABCD是矩形，MN⊥BC

∴MN⊥AD

∵点到直线的距离等于

∴EN=1

∵MN=AB=2, EC=CD=2,

∴EN=MN-EN=2-1=1

∴在Rt△ENC中，NC=

∴MD= NC=

∵由题意得：MP=MD-PD=-t,ME=MN-EN=2-1=1,EP=PD=t

∴在Rt△MPE中，

即：，解得：t=

（3）如图，当点A,点E，点C在同一条直线上时，AE最短．

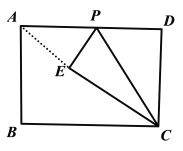
由题意得：=，EC=CD=AB=2

∴在Rt△ABC中，

∴m=AD=BC=．