题目内容
【题目】为弘扬“东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
【答案】
(1)
解:P(第一位出场是女选手)=![]()
(2)
解:列表得:
女 | 男 | 男 | 男 | |
女 | ﹣﹣﹣ | (男,女) | (男,女) | (男,女) |
男 | (女,男) | ﹣﹣﹣ | (男,男) | (男,男) |
男 | (女,男) | (男,男) | ﹣﹣﹣ | (男,男) |
男 | (女,男) | (男,男) | (男,男) | ﹣﹣﹣ |
所有等可能的情况有12种,其中第一、二位出场都是男选手的情况有6种,
则P(第一、二位出场都是男选手)=![]() =
=![]() .
.
【解析】(1)根据4位选手中女选手只有1位,求出第一位出场是女选手的概率即可;
(2)列表得出所有等可能的情况数,找出第一、二位出场都为男选手的情况数,即可求出所求的概率.
此题考查了列表法求概率的问题.

练习册系列答案
相关题目
【题目】近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数 | 100 | 60 | m |
根据以上图表信息,解答下列问题: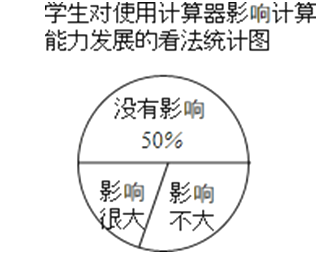
(1)统计表中的m= ;
(2)统计图中表示“影响不大”的扇形的圆心角度数为 度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?