题目内容
【题目】解不等式组
， 并把解集在数轴上表示出来．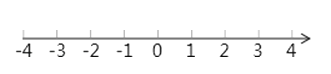
【答案】解：
解（1）得：x≥﹣1，
解（2）得：x≤2．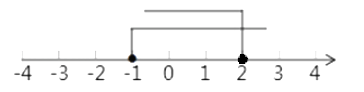
不等式组的解集是：﹣1≤x≤2．
【解析】先求出不等式组中每一个不等式的解集，然后把不等式的解集表示在数轴上，再表示出它们的公共部分即可．
【考点精析】解答此题的关键在于理解不等式的解集在数轴上的表示的相关知识，掌握不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈，以及对一元一次不等式组的解法的理解，了解解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．
练习册系列答案
相关题目
【题目】近年来，“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注，为此，某校随机调查了若干名学生对此问题的看法（看法分为三种：没有影响，影响不大，影响很大），并将调查结果绘制成如下不完整的统计表和统计图：
学生对使用计算器影响计算能力发展的看法统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数 | 100 | 60 | m |
根据以上图表信息，解答下列问题：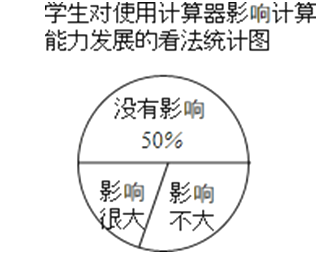
（1）统计表中的m= ；
（2）统计图中表示“影响不大”的扇形的圆心角度数为 度；
（3）从这次接受调查的学生中随机调查一人，恰好是持“影响很大”看法的概率是多少？
