Question

【题目】已知，经过点A（－4，4）的抛物线y=ax2+bx与x轴相交于点B（－3，0）．

（1）求抛物线的解析式；

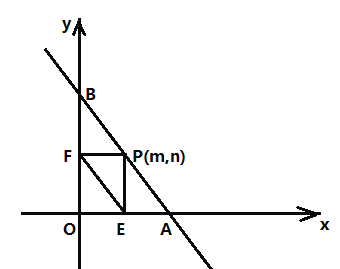
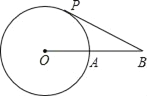
（2）如图1，过点A作AH⊥x轴，垂足为H，平行于y轴的直线交线段AO于点Q，交抛物线于点P，当四边形AHPQ为平行四边形时，求∠AOP的度数；

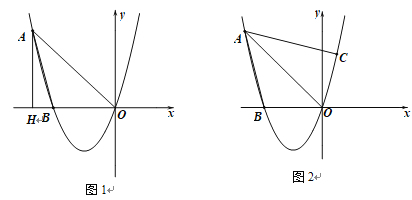
（3）如图2，，试探究：在抛物线上是否存在点C，使∠CAO＝∠BAO？若存在，请求出直线AC解析式；若不存在，请说明理由．

Answer 1

【答案】（1）y=x2+3x；（2）90°；（3）.

【解析】

（1）将点A、B、C的坐标代入抛物线的解析式求解即可；

（2）由已知A（-4，4）则可得到OA的解析式，设点P的坐标为（m，m2+3m），则点Q的坐标为（m，-m）．由题意可知QP=4，则-m-（m2+3m）=4，则可求得a的值，于是得到P（-2，-2），Q（-2，2），最后利用勾股定理的逆定理证明△OPQ为直角三角形即可；

（3）设AC交y轴于点D，根据题意证明△ABO≌△AOD，则OD=OB=3，设AC的解析式为y=px+q，将点A和点D的坐标代入求解即可．

（1）抛物线的解析式为

（2）设点P坐标为，其中

∵点A（－4，4），∴直线OA的解析式为，

从而点Q的坐标为，∴=

当四边形AHPQ为平行四边形时，PQ=AH=4，

即，解得，此时点P坐标为

∴∠AOP=∠AOH+∠POH=45o+45o=90o.

（3）设AC交y轴于点D，由点A（－4，4）得，，

∵∠CAO＝∠BAO，，∴≌

∴，点D坐标为（0，3）

设直线AC解析式为，则

解得，，∴直线AC解析式为.