题目内容
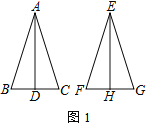
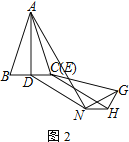
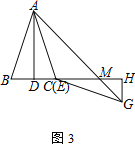
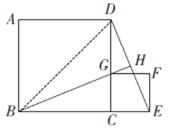
【题目】已知,如图所示,正方形![]() 的边长为1,
的边长为1,![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 与
与![]() 、
、![]() 不重合),以
不重合),以![]() 为一边向正方形
为一边向正方形![]() 外作正方形
外作正方形![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:①![]() ≌△
≌△![]() . ②
. ②![]() .
.
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)①见详解;②见详解;(2)![]()
【解析】
①根据正方形确定BC=DC,CE=CG及∠BCD=∠ECG=900,即可证明全等;
②根据(1)的全等得出∠BGC=∠DEC,再根据∠BGC+∠CBG=900,即可证得![]()
(2)根据勾股定理求出线段BD的长,然后利用三角形全等证出BE=BD,再由BE-BC求出CE即CG的长.
(1)①∵四边形![]() 与四边形
与四边形![]() 均为正方形,
均为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=900,
∴![]() ≌△
≌△![]()
②∵![]() ≌△
≌△![]() ,
,
∴∠BGC=∠DEC,
∵∠BGC+∠CBG=900,
∴∠DEC+∠CGB=900
∴∠BHE=900
即![]()
(2) 连接BD,
∵四边形ABCD是正方形,边长为1,
∴AB=AD=1,∠A=900,
∴![]()
![]()
∵BH平分DE,BH⊥DE,
∴DH=EH,∠BHD=∠BHE,
又∵BH=BH
∴△BHD≌△BHE,
∴BE=BD=![]() ,
,
∴CG=CE=BE-BC=![]() .
.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目