ΧβΡΩΡΎ»ί
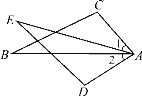
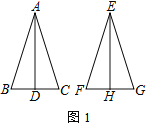
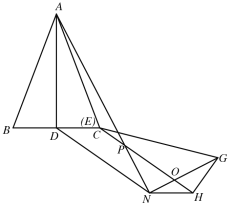
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ABΘΫACΘ§EFΘΫEGΘ§ΓςABCΓ’ΓςEFGΘ§ADΓΆBC”ΎΒψDΘ§EHΓΆFG”ΎΒψH
(1) ÷±Ϋ”–¥≥ωADΓΔEHΒΡ ΐΝΩΙΊœΒΘΚ___________________
(2) ΫΪΓςEFG―ΊEHΦτΩΣΘ§»ΟΒψEΚΆΒψC÷ΊΚœ
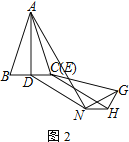
ΔΌ Α¥ΆΦ2Ζ≈÷ΟΓςEHGΘ§ΫΪœΏΕΈCD―ΊEHΤΫ“Τ÷ΝHNΘ§Ν§Ϋ”ANΓΔGNΘ§«σ÷ΛΘΚANΓΆGN
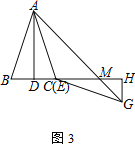
ΔΎ Α¥ΆΦ3Ζ≈÷ΟΓςEHGΘ§BΓΔCΘ®EΘ©ΓΔH»ΐΒψΙ≤œΏΘ§Ν§Ϋ”AGΫΜEH”ΎΒψMΘ°»τBDΘΫ1Θ§ADΘΫ3Θ§«σCMΒΡ≥ΛΕ»
ΓΨ¥πΑΗΓΩΘ®1Θ©AD=EHΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©CM=2.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΓςABCΓ’ΓςEFGΘ§Ω…÷ΣΟφΜΐœύΒ»Θ§άϊ”ΟΟφΜΐΙΪ ΫΩ…ΒΟΗΏœύΒ»ΘΜ
Θ®2Θ©»γΆΦΥυ ΨΘ§…ηANΓΔCHΫΜ”ΎΒψPΘ§CHΓΔNGΫΜ”ΎΒψOΘ§”…CDΤΫ“ΤΒΫNHΩ…÷ΣΥΡ±Ώ–ΈCDNHΈΣΤΫ––ΥΡ±Ώ–ΈΘ§Υυ“‘CH=DN=ADΘ§Ω…ΒΟ≥ωΓςANDΈΣΒ»―ϋ»ΐΫ«–ΈΘ§‘Ό”…GH=CD=NHΩ…ΒΟ≥ωΓςGHNΈΣΒ»―ϋ»ΐΫ«–ΈΘ§”…”ΎΝΫΗωΒ»―ϋ»ΐΫ«–ΈΕΞΫ«œύΒ»Θ§Ω…ΆΤ≥ωΒΉΫ«œύΒ»Θ§‘ΎΓςOPNΚΆΓςOGH÷–Θ§Ω…”…ΓœOPN=ΓœPND=ΓœNGHΘ§Ω…ΆΤ≥ωΓœPNO=90ΓψΘ§‘ρANΓΆGNΘΜ
Θ®3”…ADΓΆBHΘ§GHΓΆBHΘ§Ω…ΒΟADΓΈGHΘ§Υυ“‘![]() Θ§‘Ό”…DH=DC+EH=1+3=4Θ§
Θ§‘Ό”…DH=DC+EH=1+3=4Θ§
Ω…«σ≥ωDM=3Θ§ΓύCM=3-1=2.
ΫβΘΚΘ®1Θ©ΓΏΓςABCΓ’ΓςEFGΘ§
ΓύBC=FGΘ§![]()
Γύ![]()
ΓύAD=EH
Θ®2Θ©»γΆΦΥυ ΨΘ§…ηANΓΔCHΫΜ”ΎΒψPΘ§CHΓΔNGΫΜ”ΎΒψO
CDΤΫ“ΤΒΫNHΩ…ΒΟΥΡ±Ώ–ΈCDNHΈΣΤΫ––ΥΡ±Ώ–Έ
ΓύCH=DNΘ§ΓœCDN=ΓœCHNΘ§DNΓΈCH
”÷ΓΏEH=ADΘ§ΓύAD=DNΘ§Φ¥ΓςANDΈΣΒ»―ϋ»ΐΫ«–Έ
ΓΏGH=CD=NHΘ§ΓύΓςGHNΈΣΒ»―ϋ»ΐΫ«–ΈΘ§
ΓΏΓœADN=ΓœADC+ΓœCDN=90Γψ+ΓœCDN
ΓœNHG=ΓœCHG+ΓœCHN=90Γψ+ΓœCHN
ΕχΓœCDN=ΓœCHN
ΓύΓœADN=ΓœNHGΘ§
Γύ![]() Θ§
Θ§![]()
ΓύΓœAND=ΓœNGH
”÷ΓΏDNΓΈCHΘ§ΓύΓœAND=ΓœNPHΘ§ΓύΓœNGH=ΓœNPH
‘ΎΓςOPNΚΆΓςOGH÷–
ΓœNPH=ΓœNGHΘ§ΓœPON=ΓœGOHΘ§
ΓύΓœPNO=ΓœOGH=90ΓψΘ§
ΓύANΓΆGN
Θ®3Θ©”…ΓςABCΓ’ΓςEFGΩ…ΒΟCD=BD=1Θ§EH=AD=3
ÿADâBHȧGHâBH
ΓύADΓΈGHΘ§Γύ![]() Θ§Γύ
Θ§Γύ![]()
”÷ΓΏDH=DC+EH=1+3=4
ΓύDM=3Θ§
ΓύCM=DM-DC=3-1=2.