Question

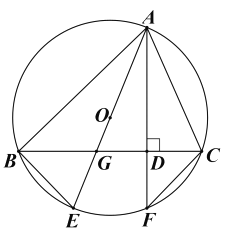
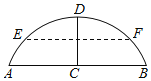
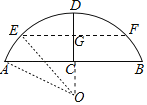
【题目】如图，有一拱桥的桥拱是圆弧形，已知桥拱的水面跨度AB（弧所对的弦的长）为8米，拱高CD（弧的中点到弦的距离）为2米．

（1）求桥拱所在圆的半径长；

（2）如果水面AB上升到EF时，从点E测得桥顶D的仰角为α，且cotα＝3，求水面上升的高度．

Answer 1

【答案】（1）桥拱所在圆的半径长为5米；（2）水面上升的高度为1米

【解析】

（1）根据点D是 中点， 知C为AB中点，联结OA，设半径OA＝OD＝R，OC＝OD﹣DC＝R﹣2，在Rt△ACO中，由勾股定理求出半径．

（2） 设OD与EF相交于点G，联结OE，由EF∥AB，OD⊥AB，得到OD⊥EF，进而找出EG＝3DG，设水面上升的高度为x米，即CG＝x，则DG＝2﹣x，在Rt△EGO中根据勾股定理求出x即可．

解：（1）∵点D是 中点，，

∴AC＝BC，DC经过圆心，

设拱桥的桥拱弧AB所在圆的圆心为O，

∵AB＝8，

∴AC＝BC＝4，

联结OA，设半径OA＝OD＝R，OC＝OD﹣DC＝R﹣2，

∵OD⊥AB，

∴∠ACO＝90°，

在Rt△ACO中，∵OA2＝AC2+OC2，

∴R2＝（R﹣2）2+42，

解之得R＝5．

答：桥拱所在圆的半径长为5米．

（2）设OD与EF相交于点G，联结OE，

∵EF∥AB，OD⊥AB，

∴OD⊥EF，

∴∠EGD＝∠EGO＝90°，

在Rt△EGD中， ，

∴EG＝3DG，

设水面上升的高度为x米，即CG＝x，则DG＝2﹣x，

∴EG＝6﹣3x，

在Rt△EGO中，∵EG2+OG2＝OE2，

∴（6﹣3x）2+（3+x）2＝52，

化简得 x2﹣3x+2＝0，解得 x1＝2（舍去），x2＝1，

答：水面上升的高度为1米．