��Ŀ����
����Ŀ���ڡ�ABC�У���C��90����AC��BC��6��
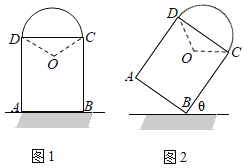
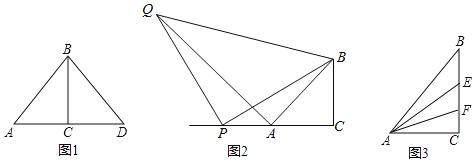
��1����ͼ1�������߶�AB�Ƶ�B��ʱ����ת90���õ��߶�BD������AD�����ABD�����Ϊ�� ����
��2����ͼ2����PΪCA�ӳ�����һ�����㣬����BP����PΪֱ�Ƕ��㣬BPΪֱ�DZ�������ֱ�ǡ�BPQ������AQ����֤��AB��AQ��
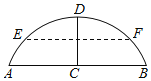
��3����ͼ3����E��FΪ�߶�BC�����㣬�ҡ�CAF����EAF����BAE����M���߶�AF��һ�����㣬��N���߶�AC��һ�����㣬�Ƿ���ڵ�M��N��ʹCM+NM��ֵ��С�������ڣ������Сֵ���������ڣ�˵�����ɣ�
���𰸡���1��36����2�������������3�����ڣ���СֵΪ3��
��������
��1��������ת�����ʵõ���ABD�ǵ���ֱ�������Σ����AD��2BC��12�����������ε������ʽ���ɵõ����ۣ�
��2����ͼ2����Q��QH��CA��CA���ӳ�����H�����ݵ���ֱ�������ε����ʣ��õ�PQ��PB����BPQ��90��������ȫ�������ε����ʵõ�PH��BC��QH��CP�����CP��AH���õ���HAQ��45�������ǵõ���BAQ��180����45����45����90�������ɵõ����ۣ�
��3��������֪�����õ���CAF����EAF����BAE��15������á�EAC��30������ͼ3������C����AF�ĶԳƵ�D����D��DN��AC��N��AF��M�����ʱ��CM+NM��ֵ��С������Сֵ��DN�����AD��AC��6������ֱ�������ε����ʼ��ɵõ����ۣ�
�⣺��1���߽��߶�AB�Ƶ�B��ʱ����ת90���õ��߶�BD��
���ABD�ǵ���ֱ�������Σ�
�ߡ�ACB��90����
��BC��AD��
��AD��2BC��12��
���ABD�������![]() ADBC��
ADBC��![]() 12��6��36��
12��6��36��
�ʴ�Ϊ��36��
��2����ͼ����Q��QH��CA��CA���ӳ�����H��

���H����C��90����
�ߡ�BPQ�ǵ���ֱ�������Σ�
��PQ��PB����BPQ��90����
���HPQ+��BPC����QPH+��PQH��90����
���PQH����BPC��
���PQH�ա�BPC��AAS����
��PH��BC��QH��CP��
��AC��BC��
��PH��AC��
��CP��AH��
��QH��AH��
���HAQ��45����
�ߡ�BAC��45����
���BAQ��180����45����45����90����
��AB��AQ��
��3����ͼ������C����AF�ĶԳƵ�D����D��DN��AC��N��AF��M��
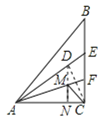
�ߡ�CAF����EAF����BAE����BAC��45����
���CAF����EAF����BAE��15����
���EAC��30����
���ʱ��CM+NM��ֵ��С������Сֵ��DN��
�ߵ�C�͵�D����AF�Գƣ�
��AD��AC��6��
�ߡ�AND��90����
��DN��![]() AD��
AD��![]() 6��3��
6��3��
��CM+NM��СֵΪ3��

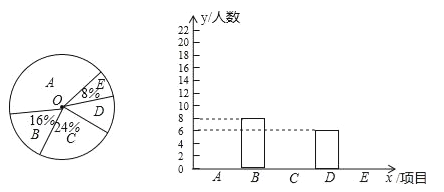
����Ŀ�����ܶ������ϲ����ͷ��Ʒ���ã���Ӱ�����彡���ָ���ͥ���Ӳ���Ҫ�Ŀ�����Ϊ��ij����ѧ��ȤС��Ա���ͬѧһ��������Ʒ����������˵��飬���¿ɷ�Ϊ���֣�A����ˮ��B��ƿװ��Ȫˮ��C��̼�����ϣ�D����̼�����ϣ�����ͳ�ƽ��������������ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ�������������
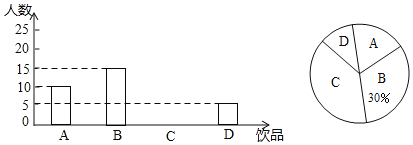
��1������༶�ж�����ͬѧ������ȫ����ͳ��ͼ��
��2�����ð�ͬѧÿ��ÿ��ֻ����һ����Ʒ��ÿ�ֽ���һƿ���۸����±�������ð�ͬѧÿ��������Ʒ���˾������Ƕ���Ԫ��
��Ʒ���� | ��ˮ | ƿװ��Ȫˮ | ̼������ | ��̼������ |
ƽ���۸�Ԫ/ƿ�� | 0 | 2 | 3 | 4 |
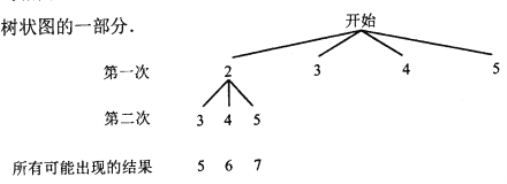
��3��Ϊ���������õ�����ϰ�ߣ������ξ��������ð�ˮ��5����ί�ɲ�����������λ���ΪA��B��������λ��ΪC��D��E���������ȡ2����ί�ɲ�������ϰ�ලԱ�������б�������״ͼ�ķ������ǡ�ó鵽2����ĸ��ʣ�