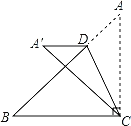
题目内容
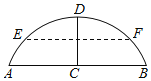
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() ;
;![]() ;(3)面积为
;(3)面积为![]() .
.
【解析】
(1)过点M作MF⊥AB于F,作MG⊥BC于G,由正方形的性质得出∠ABD=∠DBC=45°,由角平分线的性质得出MF=MG,证得四边形FBGM是正方形,得出∠FMG=90°,证出∠AMF=∠NMG,证明△AMF≌△NMG,即可得出结论;
(2)证明Rt△AMN∽Rt△BCD,得出 ,求出AN=2
,求出AN=2![]() ,由勾股定理得出BN=
,由勾股定理得出BN=![]() =4,由直角三角形的性质得出OM=OA=ON=
=4,由直角三角形的性质得出OM=OA=ON=![]() AN=
AN=![]() ,OM⊥AN,证明△PAO∽△NAB,得出
,OM⊥AN,证明△PAO∽△NAB,得出![]() ,求出OP=
,求出OP=![]() ,即可得出结果;
,即可得出结果;
(3)过点A作AF⊥BD于F,证明△AFM≌△MHN得出AF=MH,求出AF=![]() BD=
BD=![]() ×6
×6![]() =3
=3![]() ,得出MH=3
,得出MH=3![]() ,MN=2
,MN=2![]() ,由勾股定理得出HN=
,由勾股定理得出HN=![]() ,由三角形面积公式即可得出结果.
,由三角形面积公式即可得出结果.
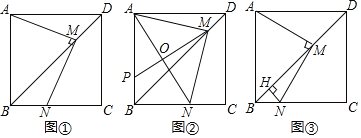
(1)证明:过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,如图①所示:
,如图①所示:

![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中, 
![]() ,
,
![]() ;
;
(2)解:在![]() 中,由(1)知:
中,由(1)知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,

在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() 在
在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即:
,即: ![]() ,
,
解得:![]() ,
,
![]() ;
;
(3)解:过点![]() 作
作![]() 于
于![]() ,如图③所示:
,如图③所示:
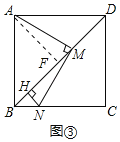
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,

![]() ,
,
![]() ,
,
在等腰直角![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() 的面积为
的面积为![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.