Question

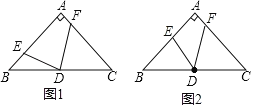
【题目】已知：△ABC，AB=AC，∠BAC=90°，点D是边BC的中点，点E在边AB上(点E不与点A、B重合)，点F在边AC上，联结DE、DF．

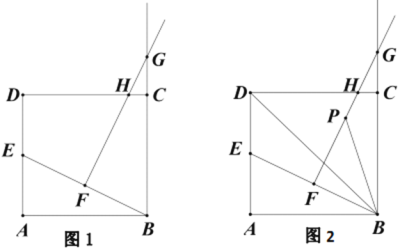
（1）如图1，当∠EDF=90°时，求证：BE=AF；

（2）如图2，当∠EDF=45°时，求证：．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）连接AD，证△BDE≌△ADF（ASA），即可得出结论；

（2）证明△BDE∽△CFD．得出，得出，由BD＝CD，即可得出结论．

（1）连接AD，如图1所示：

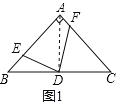
在Rt△ABC中，

∵AB=AC，∠BAC=90°，

∴∠B=∠C=45°．

∵点D是边BC的中点，

∴ADBC=BD，AD⊥BC，∠BAD=∠CAD=45°，

∴∠B=∠CAD．

∵∠EDF=90°，

∴∠ADF+∠ADE=90°

∵∠BDE+∠ADE=90°，

∴∠BDE=∠ADF，

在△BDE和△ADF中，，

∴△BDE≌△ADF(ASA)，

∴BE=AF；

（2）∵∠BDF=∠BDE+∠EDF，∠BDF=∠C+∠CFD，

∴∠BDE+∠EDF=∠C+∠CFD．

又∵∠C=∠EDF=45°，

∴∠BDE=∠CFD，

∴△BDE∽△CFD，

∴，

∴，

又∵BD=CD，

∴．