题目内容
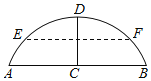
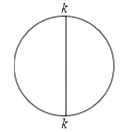
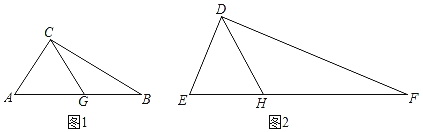
【题目】小明学习完《相似三角形》一章后,发现了一个有趣的结论:在两个不相似的直角三角形中,分别存在经过直角顶点的一条直线,把直角三角形分成两个小三角形后,如果第一个直角三角形分割出来的一个小三角形与第二个直角三角形分割出来的一个小三角形相似,那么分割出来的另外两个小三角形也相似.他把这样的两条直线称为这两个直角三角形的相似分割线.如图1、图2,直线CG、DH分别是两个不相似的Rt△ABC和Rt△DEF的相似分割线,CG、DH分别与斜边AB、EF交于点G、H,如果△BCG与△DFH相似,AC=3,AB=5,DE=4,DF=8,那么AG=_____.
【答案】3
【解析】
先由勾股定理得出BC的值,再由△BCG∽△DFH列出比例式,设AG=x,用含x的式子表示出DH;按照相似分割线可知,△AGC∽△DHE,但要先得出两个相似三角形的边或角是如何对应的,再根据相似三角形的性质列出比例式,解得x值即可.
解:∵Rt△ABC,AC=3,AB=5,
∴由勾股定理得:BC=4,
∵△BCG∽△DFH,
∴![]() =
=![]() ,
,
已知DF=8,设AG=x,则BG=5﹣x,
∴![]() =
=![]() ,
,
∴DH=10﹣2x,
∵△BCG∽△DFH,
∴∠B=∠FDH,∠BGC=∠CHF,
∴∠AGC=∠DHE,
∵∠A+∠B=90°,∠EDH+∠FDH=90°,
∴∠A=∠EDH,
∴△AGC∽△DHE,
∴![]() =
=![]() ,
,
又DE=4,
∴![]() =
=![]() ,
,
解得:x=3,
经检验,x=3是原方程的解,且符合题意.
∴AG=3.
故答案为:3.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.
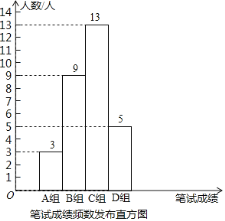
【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?