Question

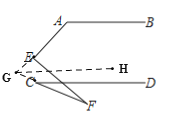
【题目】如图，AB∥CD，则∠A、∠C、∠E、∠F满足的数量关系是(　　)

A. ∠A＝∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F＝180°

C. ∠A﹣∠E+∠C+∠F＝90° D. ∠A+∠E+∠C+∠F＝360°

Answer 1

【答案】B

【解析】

延长AE、FC交与点G，过G作GH//CD，根据AB//GH得∠A+∠AGH=180°，根据GH//CD得∠FCD=∠FGH，由外角性质的∠AEF=∠AGH+∠FGH+∠F，根据等量关系整理即可的结论.

延长AE、FC交与点G，过G作GH//CD，

∵AB//CD，GH//CD，

∴AB//GH//CD，

∴∠A+∠AGH=180°，∠F=∠FCD，

∴∠AEF=∠AGH+∠FGH+∠F=180°-∠A+∠FCD+∠F，

整理得：∠A+∠AEF-∠FCD-∠F=180°，

故选B.