题目内容
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() 且与直线
且与直线![]() :
:![]() 平行,直线
平行,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C.
轴分别交于点B、C.
(1)求直线l1的表达式及其与![]() 轴的交点D的坐标;
轴的交点D的坐标;
(2)判断四边形ABCD是什么四边形?并证明你的结论;
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标,请直接写出答案.

【答案】(1)![]() (-9,0);(2)四边形ABCD是矩形;(3)(-2,-4),(10,4)
(-9,0);(2)四边形ABCD是矩形;(3)(-2,-4),(10,4)
【解析】(1)根据,直线![]() 与直线
与直线![]() 平行,设出
平行,设出![]() 的函数关系式,再利用待定系数法即可求出
的函数关系式,再利用待定系数法即可求出![]() 的函数关系式,再令
的函数关系式,再令![]() ,即可求出点D坐标;
,即可求出点D坐标;
(2)利用平面内两点间的距离公式求出AD与BC的长相等,再根据AD∥BC及BD=AC,即可求出结论;
(3)根据正方形的判定,作出图形,即可得出点E的坐标.
详解:(1)∵直线![]() 与直线
与直线![]() :
:![]() 平行,
平行,
∴设![]() ,
,
∵直线![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,
![]() ,
,
解得![]() ,
,
∴![]() .
.
(2)四边形ABCD是矩形.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵![]() ,
,![]() ,
,
∴BD=AC,
∴平行四边形ABCD是矩形.
(3)如图所示,
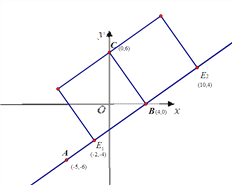
点E坐标为:![]() ,
,![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题: 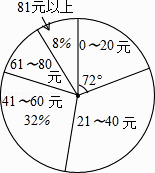
捐款 | 人数 |
0~20元 | |
21~40元 | |
41~60元 | |
61~80元 | 6 |
81元以上 | 4 |
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?