Question

【题目】如图，在中，点是的中点，且交于点，求证：是的中位线．

Answer 1

【答案】证明见解析.

【解析】

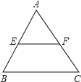
过点B作BG∥CF交FE的延长线于G，判断出四边形BCFG是平行四边形，根据平行四边形的对边相等可得BG=CF，根据两直线平行，内错角相等可得∠A=∠EBG，再利用“边角边”证明△AEF和△BEG全等，根据全等三角形对应边相等可得BG=AF，从而得到AF=CF，再根据三角形的中位线的定义证明．

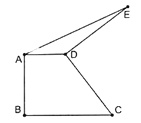
如图，过点B作BG∥CF交FE的延长线于G．

∵EF∥BC，∴四边形BCFG是平行四边形，∴BG=CF，∴BG∥CF，∴∠A=∠EBG．

∵点E是AB的中点，∴AE=BE．

在△AEF和△BEG中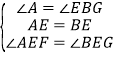，∵，∴△AEF≌△BEG（ASA），∴BG=AF，∴AF=CF．

又∵点E是AB的中点，∴EF是△ABC的中位线．