题目内容
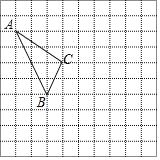
【题目】已知函数
与
轴交与
，
两点，与
轴交与
点，则能使
是直角三角形的抛物线条数是（ ）
A. 0 B. 1 C. 2 D. 3
【答案】B
【解析】
首先求出抛物线与坐标轴的交点坐标，然后利用勾股定理求出AB和BC的长，再次根据△ABC是直角三角形，利用勾股定理列出n的一元二次方程，求出n的值即可．
令y=（x﹣n）（x﹣3）=0，解得：x=n或x=3．
假设3＞n，A（3，0），B（n，0），令x=0，y=3n，即C点坐标为（0，3n），根据图形知：CB2=9+9n2，AC2=n2+9n2，AB2=（3﹣n）2，根据题意知△ABC是直角三角形，即BC2+AC2=AB2，整理得：9+9n2+n2+9n2=9﹣6n+n2，18n2+6n=0，解得：n=0或n=﹣
．
当n=0时，这样的抛物线不满足题意，即n=﹣，所以能使△ABC是直角三角形的抛物线条数是1条．
故选B．
练习册系列答案
相关题目
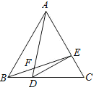
【题目】小迪同学在学勾股定理时发现一类特殊三角形：在一个三角形中，如果一个角是另一个角的2倍，那么称这个三角形为“倍角三角形”.
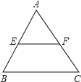
如图1，在倍角
中，
，
、
、
的对边分别记为
，
，
，三角形的三边，，有什么关系呢？让我们一起来探索……
（1）已知“倍角三角形”的一个内角为
，则这个三角形的另两个角的度数分别为______
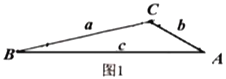
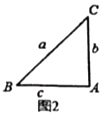
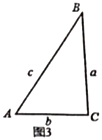
（2）小迪同学先从特殊的“倍角三角形”入手研究，请你结合图2和图3填写下表：
三角形 | 角的已知量 |
|
|
图2 |
| ______ | ______ |
图3 |
| ______ |
小迪同学根据上表，提出一般性猜想：在“倍角三角形”中，，那么，，三边满足：______；
（3）如图1：在倍角三角形中，
，、、的对边分别记为，，，求证：
.
