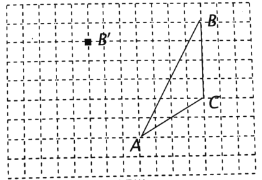
��Ŀ����
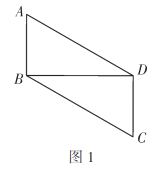
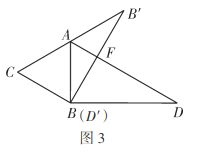
����Ŀ����ͼ��ʾ���ڳ�����ABCD�У�AB=8cm��BC=12cm��EΪAB���е㣬����P���߶�BC����4cm/s���ٶ��ɵ�B��C�˶���ͬʱ������Q���߶�CD���ɵ�C���D�˶������˶�ʱ��Ϊt��s����
��1����t=2ʱ������EBP�������
��2��������Q���붯��P��ͬ���ٶ��˶������������룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ��Ƕ��٣�
��3��������Q�ԣ�2���е��ٶȴӵ�C����������P��ԭ�����ٶȴӵ�Bͬʱ����������ʱ���س�����ABCD���ı����˶������������룬��P���Q��һ���ڳ�����ABCD����������������
���𰸡���1��S��EBP=16cm2����2������![]() �룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���
�룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s����3������9�룬��P���Q��һ���ڳ�����ABCD�ı�AB��������
cm/s����3������9�룬��P���Q��һ���ڳ�����ABCD�ı�AB��������
��������
��1��ֱ������ֱ�������������������ֱ�DZ߳˻���һ����㼴�ɣ�
��2����EBP���CQPȫ�ȣ�Ҫ�������������ۣ���EBP�ա�PCQ���EBP�ա�QCP�������t��ֵ�������Q���ٶȣ�
��3�����������⣬���ݵ�����ϵ����P�˶�·��=��Q�˶�·��+12���з�����⼴�ɣ�
��1����t=2ʱ��BP=2��4cm=8cm
��EΪAB���е㣬
��BE=![]() AB=
AB=![]() ��8cm=4cm��
��8cm=4cm��
�߳�����ABCD
���B=90��
��S��EBP=![]() BEBP=
BEBP=![]() ��4��8=16��cm2����
��4��8=16��cm2����
��2�����Q���ٶ���acm/s����BP=4t��cm����CQ=at��cm����
��PC=��12-4t����cm����
�ߡ�EBP����CQPȫ�ȣ���B=��C=90��
���EBP�ա�PCQ����EBP�ա�QCP
����EBP�ա�PCQʱ��PC=EB��CQ=BP
��12-4t=4�����t=2��
��2a=4��2
��a=4���붯��Q���붯��P��ͬ���ٶ��˶�ì�ܣ�
����EBP�ա�QCPʱ��CP=BP��CQ=BE
��12-4t=4t�����t=![]() ��
��
��![]() a=4�����a=
a=4�����a=![]() ��cm/s����
��cm/s����
�𣺾���![]() �룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���
�룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s��
cm/s��
��3���辭��x�룬��P���Q��һ���ڳ�����ABCD�ı���������
��4x=12+![]() x����ã�x=9
x����ã�x=9
��ʱ��P�˶�·��Ϊ��4��9=36��cm�������P��AB���е㴦��
�𣺾���9�룬��P���Q��һ���ڳ�����ABCD�ı�AB��������

 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д�����Ŀ��С���ֻ�Խ��Խ�ܵ����ڵ�ϲ�������ֿ�ʽ���Ͷ���г���ij�꾭Ӫ��A���ֻ�ȥ�������ܶ�Ϊ50000Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����![]() ��
��
A��B�����ֻ��Ľ��������ۼ۸����±���
A���ֻ� | B���ֻ� | |
�����۸� | 1100 | 1400 |
���ۼ۸� | ��������ۼ۸� | 2000 |
��1������A���ֻ�ÿ���ۼ۶���Ԫ��
��2���õ�ƻ��½�һ��A���ֻ���B���ֻ���60������B���ֻ��Ľ�������������A���ֻ�������������Ӧ��ν�������ʹ�����ֻ�������ࣿ