Question

【题目】综合与实践

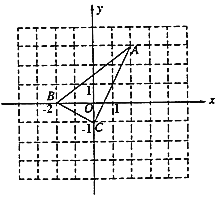
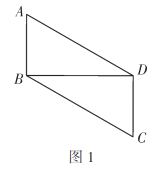
图形变换的基本方式有:平移变换、旋转变换、轴对称变换.在数学综合与实践课上，张老师将两块含角的全等三角尺按图1方式摆放在一起 ，其中.同时，要求班内各小组对图形进--步操作变换并提出问题，请你帮各小组进行解答.

[独立思考]

（1）张老师首先提出问题:图1中，四边形是平行四边形吗？说明理由；

[提出问题]

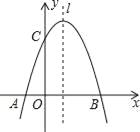
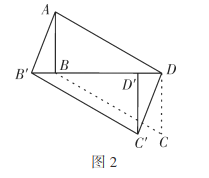
（2）如图2，“励志”小组将沿射线方向平移到的位置，分别连接，进一步提出问题：四边形是平行四边形吗？说明理由；

[拓展延伸]

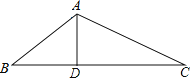
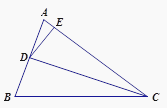
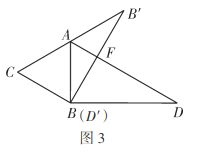
（3）“慎密”小组提出的问题是：如图3，两个全等的三角尺重叠放在的位置，将其中一个三角尺绕着点按逆时针方向旋转至的位置，使点恰好落在边上，与相交于点，若，求的长.

Answer 1

【答案】（1）四边形是平行四边形，理由见解析；（2）四边形是平行四边形，理由见解析；（3）

【解析】

（1）根据两组对边分别相等，即可判断四边形是平行四边形；

（2）根据一组对边平行且相等，即可判断四边形是平行四边形；

（3）根据题意可得，△ABC是等边三角形，可推出，可得，根据勾股定理即可得出的长．

解:（1）四边形是平行四边形，

理由：∵两块三角尺全等，

∴，

∴四边形是平行四边形；

（2）四边形是平行四边形，

理由：∵四边形是平行四边形，

∴，

且，

由平移的性质可得：，

且，

∴，

且，

∴四边形是平行四边形；

（3）∵，

∴，

∵，

∴，

∴△ABC是等边三角形，

∴，

∴，

∴，

在中，根据勾股定理得，

∴的长为．