题目内容
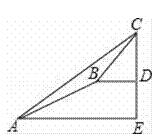
【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8.
(1)求DE的长;
(2)求△ADB的面积.

【答案】(1)3;(2)15
【解析】
(1)根据勾股定理求出AB,根据角平分线的性质得到CD=DE,根据三角形的面积公式求出DE;
(2)根据三角形的面积公式计算.
(1)∵在Rt△ABC中,∠C=90°,AC=6,BC=8
∴AB=10
又∵AD平分∠CAB,DE⊥AB于E
∴DE=CD,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE=6
∴BE=AB-AE=4
BD=BC-CD=8-DE
在Rt△DEB中,BD2=DE2+BE2
即(8-DE)2=DE2+42
解得:DE=3
(2)S△ADB=![]() ×AB×DE=
×AB×DE=![]() ×10×3=15
×10×3=15

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及.
(1) 为获得东台市市民参与共享经济的活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同社区,选取部分市民进行问卷调查
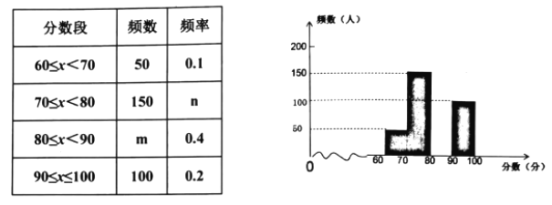
(2) 调查小组随机调查了东台市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.
骑共享单车的人数统计表
年龄段(岁) | 频数 | 频率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
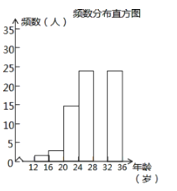
根据以上信息解答下列问题:
① 求出统计表中的a、b,并补全频数分布直方图;
② 试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?