题目内容
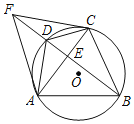
【题目】在正方形
和等腰直角
中，
，
是
的中点，连接
、
.
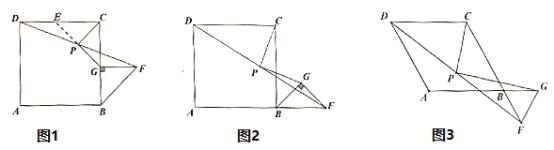
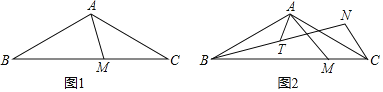
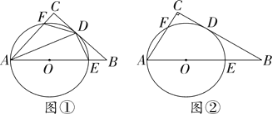
（1）如图1，当点
在
边上时，延长
交
于点
.求证：
；
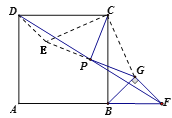
（2）如图2，当点
在
的延长线上时，（1）中的结论是否成立？请证明你的结论；
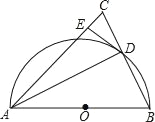
（3）如图3，若四边形为菱形，且
，为等边三角形，点在
的延长线上时，线段、又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线.
【答案】（1）证明见解析；（2）成立，证明见解析；（3）
，图详见解析.
【解析】
（1）利用已知条件易证
，则有
，
，从而有
，再利用直角三角形的斜边中线的性质即可得出结论；
（2）由已知条件易证，由全等三角形的性质证明
，最后利用直角三角形的斜边中线的性质即可得出结论；
（3）由已知条件易证，由全等三角形的性质证明
，最后利用等腰三角形的性质和特殊角的三角函数值即可求出答案.
（1）证明：
，
又
，
(ASA)
，
又
，
，
在
中，
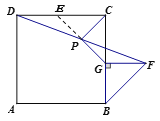
（2）成立，证明如下：
延长
到
，使，连接
、
、
.
，，
、、
，
，
，
在中，
（3）
论证过程中需要的辅助线如图所示
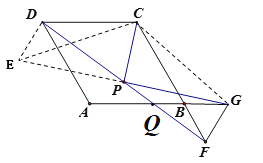
证明：延长GP到点E，使
,连接DE，CE,CG,
∵
∴
∴
∵
为等边三角形
∴
∴
∵
∴
∴
∵
∴
∵
∴
又∵
∴
∴
又∵
∴
∵
∴
∴
∴
练习册系列答案
相关题目
