Question

【题目】如图，四边形ABCD内接与⊙O，AB=AC，AC⊥BD，垂足为E，点F在BD的延长线上，且DF=DC，连接AF、CF。

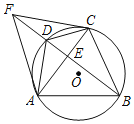
（1）若∠CAD=α，求∠BAC（用含α的代数式表示）；

（2）求证：CF是⊙O的切线。

Answer 1

【答案】（1）∠BAC=2α；（2）见解析

【解析】

（1）根据等腰三角形的性质得出∠ABC=∠ACB，根据圆心角、弧、弦的关系得到，即可得到∠ABC=∠ADB，根据三角形内角和定理得到∠ABC=（180°-∠BAC）=90°-∠BAC，∠ADB=90°-∠CAD，从而得到∠BAC=∠CAD，即可证得结论；

（2）连接OA，OC，设∠CAD=α，∠ABD=β，则可得∠AOC=2(α+β)，从而可求出∠ACO=90°-α-β，由圆周角定理可得∠BDC=2α，因为DF=DC，所以∠DCF=∠DFC=α,可求得∠DCF+∠DCA+∠DCO=90°，从而可得结论.

（1）∵AB=AC，

∴，∠ABC=∠ACB，

∴∠ABC=∠ADB，∠ABC=（180°-∠BAC）=90°-∠BAC，

∵BD⊥AC，

∴∠ADB=90°-∠CAD，

∴∠BAC=∠CAD，

∴∠BAC=2∠CAD；

∵∠CAD=α，

∴∠BAC=2α;

（2）连接OA，OC，设∠CAD=α，∠ABD=β，

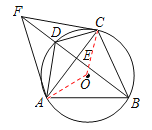
∴∠ABC=α+β，∠ACD=β

∴∠AOC=2(α+β)，

∵AO=OC

∴∠ACO=，

由（1）得∠BAC=2α，

∴∠BDC=2α

∵DF=DC

∴∠DFC=∠DCF，

∴∠DFC+∠DCF=2α，即∠DCF=α，

∵∠OCF=∠OCA+∠ACD+∠DCF=90°-α-β+β+α=90°，

∴OC⊥FC，

∴CF是⊙O的切线.