题目内容
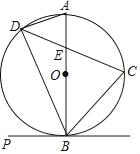
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)当⊙O半径为3,CE=2时,求BD长.
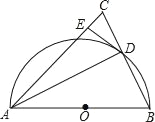
【答案】(1)证明见解析;(2)BD=2![]() .
.
【解析】
(1)连接OD,AB为⊙0的直径得∠ADB=90°,由AB=AC,根据等腰三角形性质得AD平分BC,即DB=DC,则OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,则OD⊥DE,然后根据切线的判定方法即可得到结论;
(2)由∠B=∠C,∠CED=∠BDA=90°,得出△DEC∽△ADB,得出![]() ,从而求得BDCD=ABCE,由BD=CD,即可求得BD2=ABCE,然后代入数据即可得到结果.
,从而求得BDCD=ABCE,由BD=CD,即可求得BD2=ABCE,然后代入数据即可得到结果.
(1)证明:连接OD,如图,
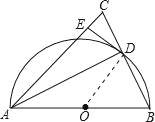
∵AB为⊙0的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分BC,即DB=DC,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙0的切线;
(2)∵∠B=∠C,∠CED=∠BDA=90°,
∴△DEC∽△ADB,
∴![]() ,
,
∴BDCD=ABCE,
∵BD=CD,
∴BD2=ABCE,
∵⊙O半径为3,CE=2,
∴BD=![]() =2
=2![]() .
.

练习册系列答案
相关题目