题目内容
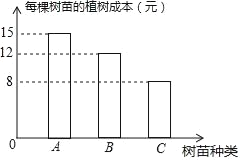
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)先求出种植C种树苗的人数,根据现种植A、B、C三种树苗一共480棵,可以列出等量关系,解出y与x之间的关系;
(2)①分别求出种植A,B,C三种树苗的成本,然后相加即可;
②求出种植C种树苗工人的人数,然后用种植C种树苗工人的人数÷总人数即可求出概率.
解:(1)设种植A种树苗的工人为x名,种植B种树苗的工人为y名,则种植C种树苗的人数为(80-x-y)人,
根据题意,得:8x+6y+5(80-x-y)=480,
整理,得:y=-3x+80;
(2)①w=15×8x+12×6y+8×5(80-x-y)=80x+32y+3200,
把y=-3x+80代入,得:w=-16x+5760,
②种植的总成本为5600元时,w=-16x+5760=5600,
解得x=10,y=-3×10+80=50,
即种植A种树苗的工人为10名,种植B种树苗的工人为50名,种植B种树苗的工人为:80-10-50=20名.
采访到种植C种树苗工人的概率为:![]() =
=![]() .
.

练习册系列答案
相关题目