题目内容
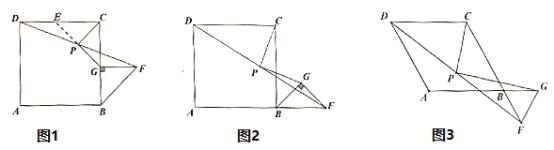
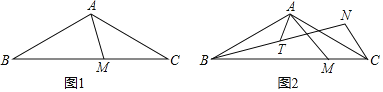
【题目】在△ABC中,AB=AC,∠BAC=120°,M为BC边上一动点(M不与B、C重合)
(1)如图1,若∠MAC=45°,求![]() ;
;
(2)如图2,将CM绕点C顺时针旋转60°至CN,连接BN,T为BN的中点,连接AT.
①求证:AM=2AT;
②当AB=AC=2时,直接写出CM+4AT的最小值为 .
【答案】(1)![]() ;(2)①见解析;②2
;(2)①见解析;②2![]()
【解析】
(1)如图1,过点M作MH⊥AC于H,证△AMH是等腰直角三角形,设AH=a,则MH=a,在Rt△CMH中,求出CH,CM的长,再证BM=AC即可求出结果;
(2)①如图2﹣1,延长BA至Q且使AQ=AB,连接CQ,MN,AN,NQ,证△ACQ和△MCN为等边三角形,推出AN=QN=AM,由三角形的中位线定理即可推出结论;
②如图2﹣2,将△QCN绕点C顺时针旋转60°得到△Q'CN',连接NN',MN,QQ',AQ',设AQ'与QC交于点G,推出CM+4AT=CN+AN+NQ=NN'+AN+N'Q',即当A,N,N',Q'在一条直线上时,CM+4AT有最小值,为AQ'的长度,求出AQ'的长度即可.
(1)解:如图1,过点M作MH⊥AC于H,
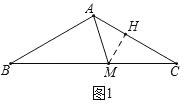
∵∠MAC=45°,
∴△AMH是等腰直角三角形,
设AH=a,则MH=a,
∵AB=AC,∠BAC=120°,
∴∠C=30°,
∴在Rt△CMH中,
CH=![]() MH=
MH=![]() ,CM=2MH=2a,
,CM=2MH=2a,
∴AC=AH+CH=(1+![]() )a,
)a,
∵∠BAM=∠BAC﹣∠CAM=75°,∠BMA=∠C+∠CAM=75°,
∴∠BAM=∠BMA,
∴BM=AB=AC=(1+![]() )a,
)a,
∴![]() ;
;
(2)①证明:如图2﹣1,延长BA至Q且使AQ=AB,连接CQ,MN,AN,NQ
则AC=AQ,
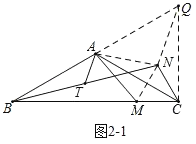
∵∠CAQ=180°﹣∠BAC=60°,
∴△ACQ为等边三角形,
∵CM=CN,∠MCN=60°,
∴△MCN为等边三角形,
∵∠ACM=30°,
∴∠ACN=60°﹣∠ACM=30°,∠QCN=60°﹣∠ACN=30°,
∴AC垂直平分MN,
∵AM=AN,
又∵AC=QC,∠ACN=∠QCN,CN=CN,
∴△ACN≌△QCN(SAS),
∴AN=QN,
∴AM=QN,
∵BA=QA,BT=NT,
∴QN=2AT,
即AM=2AT;
②解:如图2﹣2,将△QCN绕点C顺时针旋转60°得到△Q'CN',连接NN',MN,QQ',AQ',设AQ'与QC交于点G,
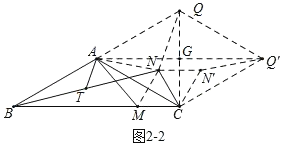
则∠NCN'=∠QCQ'=60°,NQ=N'Q',
又∵CN=CN',CQ=CQ',
∴△CNN'与△CQQ'是等边三角形,
由①知AN=NQ=AM=2AT,
∴CM+4AT=CN+AN+NQ=NN'+AN+N'Q',
即当A,N,N',Q'在一条直线上时,CM+4AT有最小值,为AQ'的长度,
∵△ACQ和△CQQ'是等边三角形,
∴AC=AQ=CQ=QQ'=CQ'=2,
∴四边形ACQ'Q为菱形,
∴AQ'⊥CQ,
∴在Rt△AQG中,
AG=![]() AQ=
AQ=![]() ,
,
∴AQ'=2AG=2![]() ,
,
故答案为:2![]() .
.

 阅读快车系列答案
阅读快车系列答案