题目内容
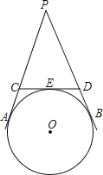
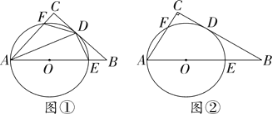
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
【答案】(1)∠B=40°;(2)AB= 6.
【解析】
(1)连接OD,由在△ABC中, ∠C=90°,BC是切线,易得AC∥OD,即可求得∠CAD=∠ADO,继而求得答案;
(2)首先连接OF,OD,由AC∥OD得∠OFA=∠FOD,由点F为弧AD的中点,易得△AOF是等边三角形,继而求得答案.
解:(1)如解图①,连接OD,
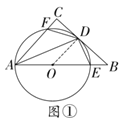
∵BC切⊙O于点D,
∴∠ODB=90°,
∵∠C=90°,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠DAO=∠ADO=∠CAD=25°,
∴∠DOB=∠CAO=∠CAD+∠DAO=50°,
∵∠ODB=90°,
∴∠B=90°-∠DOB=90°-50°=40°;
(2)如解图②,连接OF,OD,
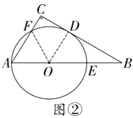
∵AC∥OD,
∴∠OFA=∠FOD,
∵点F为弧AD的中点,
∴∠AOF=∠FOD,
∴∠OFA=∠AOF,
∴AF=OA,
∵OA=OF,
∴△AOF为等边三角形,
∴∠FAO=60°,则∠DOB=60°,
∴∠B=30°,
∵在Rt△ODB中,OD=2,
∴OB=4,
∴AB=AO+OB=2+4=6.

练习册系列答案
相关题目